Soluciones para el desafío del generador de series de números:parte 4

Esta es la cuarta parte de una serie sobre soluciones al desafío del generador de series numéricas. Muchas gracias a Alan Burstein, Joe Obbish, Adam Machanic, Christopher Ford, Jeff Moden, Charlie, NoamGr, Kamil Kosno, Dave Mason, John Nelson #2, Ed Wagner, Michael Burbea y Paul White por compartir sus ideas y comentarios.

Me encanta el trabajo de Paul White. Sigo sorprendiéndome por sus descubrimientos, y me pregunto cómo diablos se da cuenta de lo que hace. También me encanta su estilo de escritura eficiente y elocuente. A menudo, mientras leo sus artículos o publicaciones, niego con la cabeza y le digo a mi esposa, Lilach, que cuando sea grande quiero ser como Paul.

Cuando publiqué originalmente el desafío, esperaba en secreto que Paul publicara una solución. Sabía que si lo hacía, sería muy especial. Bueno, lo hizo, ¡y es fascinante! Tiene un rendimiento excelente, y hay mucho que puedes aprender de él. Este artículo está dedicado a la solución de Paul.

Haré mis pruebas en tempdb, habilitando E/S y estadísticas de tiempo:

SET NOCOUNT ON;
 
USE tempdb;
 
SET STATISTICS TIME, IO ON;

Limitaciones de ideas anteriores

Al evaluar las soluciones anteriores, uno de los factores importantes para obtener un buen rendimiento fue la capacidad de emplear el procesamiento por lotes. Pero, ¿lo hemos explotado al máximo posible?

Examinemos los planes de dos de las soluciones anteriores que utilizaban el procesamiento por lotes. En la Parte 1 cubrí la función dbo.GetNumsAlanCharlieItzikBatch, que combinaba ideas de Alan, Charlie y mías.

Aquí está la definición de la función:

-- Helper dummy table
DROP TABLE IF EXISTS dbo.BatchMe;
GO
 
CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
GO
 
-- Function definition
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE
AS
RETURN
  WITH
    L0 AS ( SELECT 1 AS c
            FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
                        (1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
    L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
    L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
    L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
    Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
              FROM L3 )
  SELECT TOP(@high - @low + 1)
     rownum AS rn,
     @high + 1 - rownum AS op,
 
     @low - 1 + rownum AS n
  FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
  ORDER BY rownum;
GO

Esta solución define un constructor de valores de tabla base con 16 filas y una serie de CTE en cascada con uniones cruzadas para inflar el número de filas a 4B potencialmente. La solución usa la función ROW_NUMBER para crear la secuencia base de números en un CTE llamado Nums, y el filtro TOP para filtrar la cardinalidad de la serie numérica deseada. Para habilitar el procesamiento por lotes, la solución utiliza una unión izquierda ficticia con una condición falsa entre el Nums CTE y una tabla denominada dbo.BatchMe, que tiene un índice de almacén de columnas.

Use el siguiente código para probar la función con la técnica de asignación de variables:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);

La representación del Plan Explorer del real el plan para esta ejecución se muestra en la Figura 1.

Figura 1:Plan para la función dbo.GetNumsAlanCharlieItzikBatch

Al analizar el procesamiento en modo por lotes frente al modo en fila, es bastante bueno poder saber con solo mirar un plan a un nivel alto qué modo de procesamiento usó cada operador. De hecho, Plan Explorer muestra una figura de lote azul claro en la parte inferior izquierda del operador cuando su modo de ejecución real es Lote. Como puede ver en la Figura 1, el único operador que utilizó el modo por lotes es el operador Agregado de ventana, que calcula los números de fila. Todavía hay mucho trabajo realizado por otros operadores en el modo fila.

Estos son los números de rendimiento que obtuve en mi prueba:

lecturas lógicas 0

Para identificar qué operadores tardaron más en ejecutarse, use la opción Plan de ejecución real en SSMS o la opción Obtener plan real en Plan Explorer. Asegúrese de leer el artículo reciente de Paul Comprender los tiempos del operador del plan de ejecución. El artículo describe cómo normalizar los tiempos de ejecución del operador informados para obtener los números correctos.

En el plan de la Figura 1, la mayor parte del tiempo lo dedican los operadores Nested Loops y Top que se encuentran más a la izquierda, ambos ejecutándose en modo de fila. Además de que el modo de fila es menos eficiente que el modo por lotes para las operaciones intensivas de la CPU, también tenga en cuenta que cambiar del modo de fila al modo por lotes y viceversa tiene un costo adicional.

En la Parte 2, cubrí otra solución que empleaba procesamiento por lotes, implementada en la función dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2. Esta solución combinó ideas de John Number2, Dave Mason, Joe Obbish, Alan, Charlie y yo. La principal diferencia entre la solución anterior y esta es que, como unidad base, la primera usa un constructor de valores de tabla virtual y la segunda usa una tabla real con un índice de almacén de columnas, lo que le brinda procesamiento por lotes "gratis". Aquí está el código que crea la tabla y la llena usando una declaración INSERT con 102,400 filas para comprimirla:

DROP TABLE IF EXISTS dbo.NullBits102400;
GO
 
CREATE TABLE dbo.NullBits102400
(
  b BIT NULL, 
  INDEX cc_NullBits102400 CLUSTERED COLUMNSTORE
    WITH (DATA_COMPRESSION = COLUMNSTORE_ARCHIVE)
);
GO
 
WITH
  L0 AS (SELECT CAST(NULL AS BIT) AS b
         FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1)) AS D(b)),
  L1 AS (SELECT A.b FROM L0 AS A CROSS JOIN L0 AS B),
  nulls(b) AS (SELECT A.b FROM L1 AS A CROSS JOIN L1 AS B CROSS JOIN L1 AS C)
INSERT INTO dbo.NullBits102400 WITH (TABLOCK) (b) 
  SELECT TOP(102400) b FROM nulls;
GO

Aquí está la definición de la función:

CREATE OR ALTER FUNCTION dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2
  (@low AS BIGINT = 1, @high AS BIGINT) RETURNS TABLE
AS
RETURN
  WITH
    Nums AS (SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
             FROM dbo.NullBits102400 AS A
               CROSS JOIN dbo.NullBits102400 AS B)
  SELECT TOP(@high - @low + 1)
     rownum AS rn,
     @high + 1 - rownum AS op,
     @low - 1 + rownum AS n
  FROM Nums
  ORDER BY rownum;
GO

Una sola combinación cruzada entre dos instancias de la tabla base es suficiente para producir mucho más allá del potencial deseado de 4B filas. Nuevamente aquí, la solución usa la función ROW_NUMBER para producir la secuencia base de números y el filtro TOP para restringir la cardinalidad deseada de la serie numérica.

Aquí está el código para probar la función usando la técnica de asignación de variables:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2(1, 100000000) OPTION(MAXDOP 1);

El plan para esta ejecución se muestra en la Figura 2.

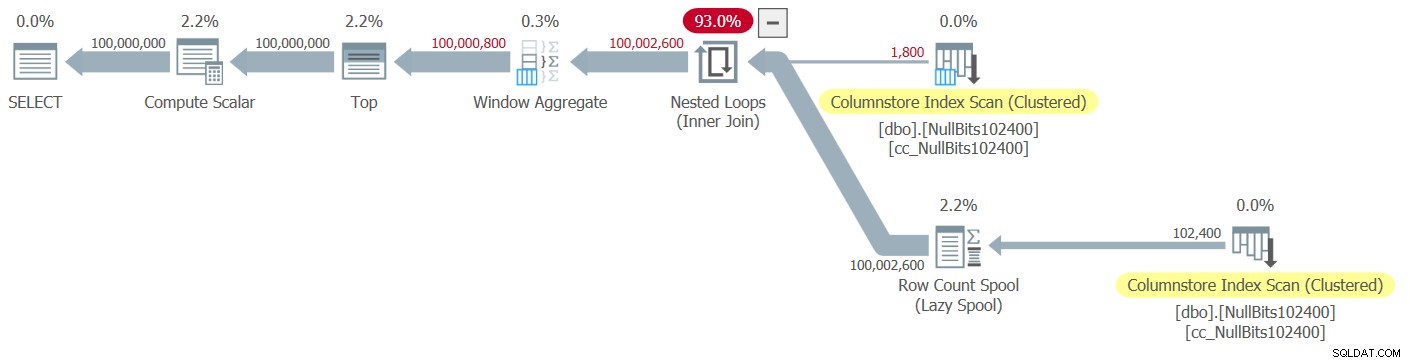Figura 2:Plan para la función dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2

Observe que solo dos operadores en este plan utilizan el modo por lotes:el escaneo superior del índice de almacén de columnas agrupado de la tabla, que se usa como la entrada externa de la combinación de bucles anidados, y el operador Agregado de ventana, que se usa para calcular los números de fila base. .

Obtuve los siguientes números de rendimiento para mi prueba:

Tabla 'NullBits102400'. Recuento de escaneos 2, lecturas lógicas 0, lecturas físicas 0, lecturas del servidor de páginas 0, lecturas anticipadas 0, lecturas anticipadas del servidor de páginas 0, lecturas lógicas lob 8, lecturas físicas lob 0, lecturas del servidor de páginas lob 0, lecturas lob- adelante lee 0, la lectura anticipada del servidor de páginas de lob lee 0.

Tabla 'NullBits102400'. El segmento lee 2, el segmento omitió 0.

Una vez más, la mayor parte del tiempo en la ejecución de este plan lo dedican los operadores Nested Loops y Top de más a la izquierda, que se ejecutan en modo de fila.

La solución de Pablo

Antes de presentar la solución de Paul, comenzaré con mi teoría sobre el proceso de pensamiento por el que pasó. Este es realmente un gran ejercicio de aprendizaje, y le sugiero que lo haga antes de buscar la solución. Paul reconoció los efectos debilitantes de un plan que combina los modos por lotes y por filas, y se planteó el desafío de encontrar una solución que tenga un plan de modo por lotes. Si tiene éxito, el potencial de que dicha solución funcione bien es bastante alto. Sin duda, es intrigante ver si tal objetivo es alcanzable dado que todavía hay muchos operadores que aún no admiten el modo por lotes y muchos factores que inhiben el procesamiento por lotes. Por ejemplo, en el momento de escribir este artículo, el único algoritmo de combinación que admite el procesamiento por lotes es el algoritmo de combinación hash. Una unión cruzada se optimiza mediante el algoritmo de bucles anidados. Además, el operador Top se implementa actualmente solo en modo fila. Estos dos elementos son elementos fundamentales críticos utilizados en los planes para muchas de las soluciones que cubrí hasta ahora, incluidas las dos anteriores.

Suponiendo que le haya dado una oportunidad decente al desafío de crear una solución con un plan de modo por lotes, pasemos al segundo ejercicio. Primero presentaré la solución de Paul tal como la proporcionó, con sus comentarios en línea. También lo ejecutaré para comparar su rendimiento con las otras soluciones. Aprendí mucho deconstruyendo y reconstruyendo su solución, paso a paso, para asegurarme de entender cuidadosamente por qué utilizó cada una de las técnicas que utilizó. Te sugiero que hagas lo mismo antes de pasar a leer mis explicaciones.

Esta es la solución de Paul, que involucra una tabla auxiliar de almacén de columnas llamada dbo.CS y una función llamada dbo.GetNums_SQLkiwi:

-- Helper columnstore table
DROP TABLE IF EXISTS dbo.CS;
 
-- 64K rows (enough for 4B rows when cross joined)
-- column 1 is always zero
-- column 2 is (1...65536)
SELECT
    -- type as integer NOT NULL
    -- (everything is normalized to 64 bits in columnstore/batch mode anyway)
    n1 = ISNULL(CONVERT(integer, 0), 0), 
    n2 = ISNULL(CONVERT(integer, N.rn), 0)
INTO dbo.CS
FROM 
(
    SELECT
        rn = ROW_NUMBER() OVER (ORDER BY @@SPID)
    FROM master.dbo.spt_values AS SV1
    CROSS JOIN master.dbo.spt_values AS SV2
    ORDER BY 
        rn ASC
        OFFSET 0 ROWS
        FETCH NEXT 65536 ROWS ONLY
) AS N;
 
-- Single compressed rowgroup of 65,536 rows
CREATE CLUSTERED COLUMNSTORE INDEX CCI 
ON dbo.CS 
WITH (MAXDOP = 1);
GO
 
-- The function
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT 
            -- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            -- Batch mode hash cross join
            -- Integer not null data type avoid hash probe residual
            -- This is always 0 = 0
            ON N2.n1 = N1.n1
        WHERE
            -- Try to avoid SQRT on negative numbers and enable simplification 
            -- to single constant scan if @low > @high (with literals)
            -- No start-up filters in batch mode
            @high >= @low
            -- Coarse filter:
            -- Limit each side of the cross join to SQRT(target number of rows)
            -- IIF avoids SQRT on negative numbers with parameters
            AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
    ) AS N
    WHERE
        -- Precise filter:
        -- Batch mode filter the limited cross join to the exact number of rows needed
        -- Avoids the optimizer introducing a row-mode Top with following row mode compute scala
        @low - 2 + N.rn < @high;
GO

Aquí está el código que usé para probar la función con la técnica de asignación de variables:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000);

Obtuve el plan que se muestra en la Figura 3 para mi prueba.

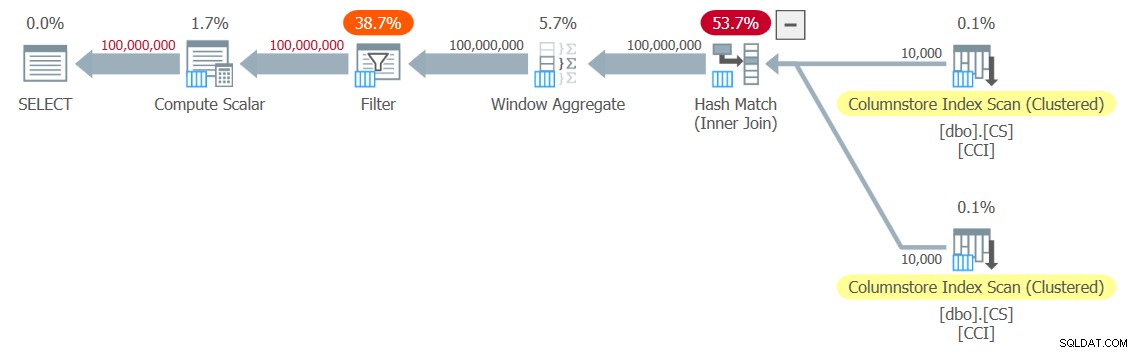Figura 3:Plan para la función dbo.GetNums_SQLkiwi

¡Es un plan de modo por lotes! Eso es bastante impresionante.

Estos son los números de rendimiento que obtuve para esta prueba en mi máquina:

Tabla 'CS'. Recuento de escaneos 2, lecturas lógicas 0, lecturas físicas 0, lecturas del servidor de páginas 0, lecturas anticipadas 0, lecturas anticipadas del servidor de páginas 0, lecturas lógicas lob 44, lecturas físicas lob 0, lecturas del servidor de páginas lob 0, lecturas lob- adelante lee 0, la lectura anticipada del servidor de páginas de lob lee 0.

Tabla 'CS'. El segmento lee 2, el segmento omitió 0.

También verifiquemos que si necesita devolver los números ordenados por n, la solución conserva el orden con respecto a rn, al menos cuando se usan constantes como entradas, y así evita la clasificación explícita en el plan. Aquí está el código para probarlo con order:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000) ORDER BY n;

Obtiene el mismo plan que en la Figura 3 y, por lo tanto, cifras de rendimiento similares:

Tabla 'CS'. Recuento de escaneos 2, lecturas lógicas 0, lecturas físicas 0, lecturas del servidor de páginas 0, lecturas anticipadas 0, lecturas anticipadas del servidor de páginas 0, lecturas lógicas lob 44, lecturas físicas lob 0, lecturas del servidor de páginas lob 0, lecturas lob- adelante lee 0, la lectura anticipada del servidor de páginas de lob lee 0.

Tabla 'CS'. El segmento lee 2, el segmento omitió 0.

Ese es un aspecto importante de la solución.

Cambiando nuestra metodología de prueba

El rendimiento de la solución de Paul es una mejora decente tanto en el tiempo transcurrido como en el tiempo de la CPU en comparación con las dos soluciones anteriores, pero no parece la mejora más dramática que uno esperaría de un plan de modo por lotes. ¿Quizás nos estamos perdiendo algo?

Probemos y analicemos los tiempos de ejecución del operador observando el Plan de ejecución real en SSMS como se muestra en la Figura 4.

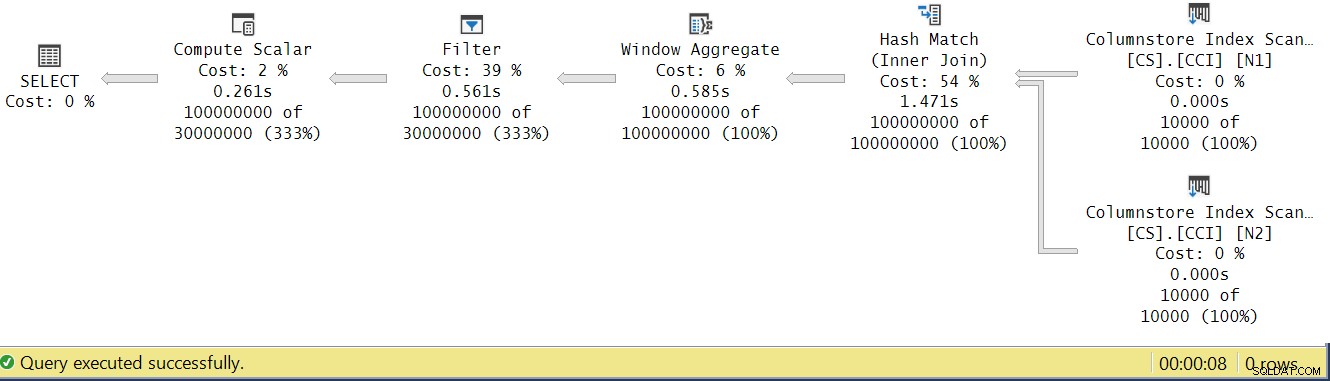Figura 4:tiempos de ejecución del operador para la función dbo.GetNums_SQLkiwi

En el artículo de Paul sobre el análisis de los tiempos de ejecución del operador, explica que con los operadores en modo por lotes, cada uno informa su propio tiempo de ejecución. Si suma los tiempos de ejecución de todos los operadores en este plan real, obtendrá 2,878 segundos, pero el plan tardó 7,876 en ejecutarse. Parece que faltan 5 segundos del tiempo de ejecución. La respuesta a esto radica en la técnica de prueba que estamos usando, con la asignación de variables. Recuerde que decidimos usar esta técnica para eliminar la necesidad de enviar todas las filas desde el servidor a la persona que llama y para evitar las E/S que estarían involucradas al escribir el resultado en una tabla. Parecía la opción perfecta. Sin embargo, el verdadero costo de la asignación de variables está oculto en este plan y, por supuesto, se ejecuta en modo fila. Misterio resuelto.

Obviamente, al final del día, una buena prueba es una prueba que refleja adecuadamente su uso de producción de la solución. Si normalmente escribe los datos en una tabla, necesita que su prueba lo refleje. Si envía el resultado a la persona que llama, necesita que su prueba lo refleje. En cualquier caso, la asignación de variables parece representar una gran parte del tiempo de ejecución en nuestra prueba y claramente es poco probable que represente el uso típico de producción de la función. Paul sugirió que, en lugar de la asignación de variables, la prueba podría aplicar un agregado simple como MAX a la columna de números devueltos (n/rn/op). Un operador agregado puede utilizar el procesamiento por lotes, por lo que el plan no implicaría la conversión del modo por lotes al modo de filas como resultado de su uso, y su contribución al tiempo de ejecución total debería ser bastante pequeña y conocida.

Así que volvamos a probar las tres soluciones cubiertas en este artículo. Aquí está el código para probar la función dbo.GetNumsAlanCharlieItzikBatch:

SELECT MAX(n) AS mx FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);

Obtuve el plan que se muestra en la Figura 5 para esta prueba.

Figura 5:Plan para la función dbo.GetNumsAlanCharlieItzikBatch con agregado

Aquí están los números de rendimiento que obtuve para esta prueba:

lecturas lógicas 0

Observe que el tiempo de ejecución se redujo de 10,025 segundos con la técnica de asignación de variables a 8,733 con la técnica agregada. Eso es un poco más de un segundo de tiempo de ejecución que podemos atribuir a la asignación de variables aquí.

Aquí está el código para probar la función dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2:

SELECT MAX(n) AS mx FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2(1, 100000000) OPTION(MAXDOP 1);

Obtuve el plan que se muestra en la Figura 6 para esta prueba.

Figura 6:Plan para la función dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2 con agregado

Aquí están los números de rendimiento que obtuve para esta prueba:

Tabla 'NullBits102400'. Recuento de escaneos 2, lecturas lógicas 0, lecturas físicas 0, lecturas del servidor de páginas 0, lecturas anticipadas 0, lecturas anticipadas del servidor de páginas 0, lecturas lógicas lob 8, lecturas físicas lob 0, lecturas del servidor de páginas lob 0, lecturas lob- adelante lee 0, la lectura anticipada del servidor de páginas de lob lee 0.

Tabla 'NullBits102400'. El segmento lee 2, el segmento omitió 0.

Observe que el tiempo de ejecución se redujo de 9,813 segundos con la técnica de asignación de variables a 7,053 con la técnica agregada. Eso es un poco más de dos segundos de tiempo de ejecución que podemos atribuir a la asignación de variables aquí.

Y aquí está el código para probar la solución de Paul:

SELECT MAX(n) AS mx FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(MAXDOP 1);

Obtengo el plan que se muestra en la Figura 7 para esta prueba.

Figura 7:Plan para la función dbo.GetNums_SQLkiwi con agregado

Y ahora el gran momento. Obtuve los siguientes números de rendimiento para esta prueba:

Tabla 'CS'. Recuento de escaneos 2, lecturas lógicas 0, lecturas físicas 0, lecturas del servidor de páginas 0, lecturas anticipadas 0, lecturas anticipadas del servidor de páginas 0, lecturas lógicas lob 44, lecturas físicas lob 0, lecturas del servidor de páginas lob 0, lecturas lob- adelante lee 0, la lectura anticipada del servidor de páginas de lob lee 0.

Tabla 'CS'. El segmento lee 2, el segmento omitió 0.

¡El tiempo de ejecución se redujo de 7,822 segundos a 3,149 segundos! Examinemos los tiempos de ejecución del operador en el plan real en SSMS, como se muestra en la Figura 8.

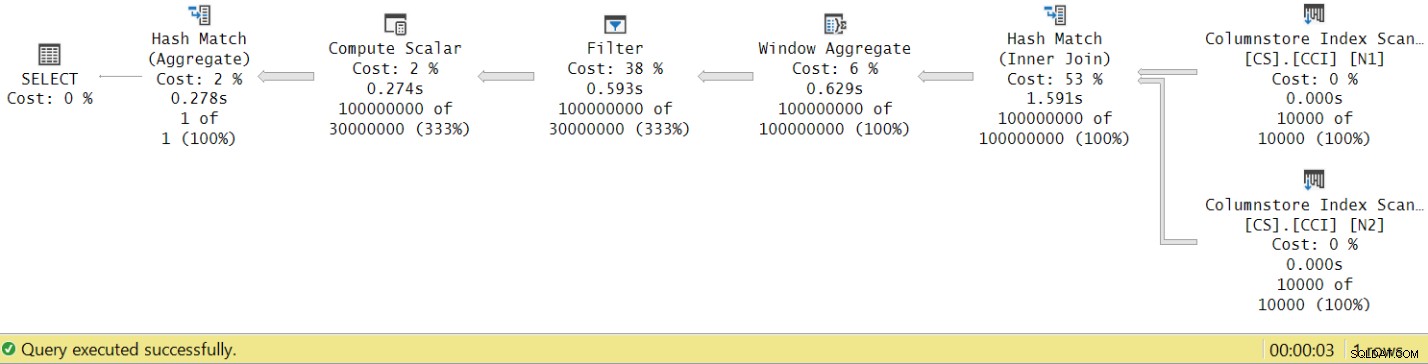Figura 8:tiempos de ejecución del operador para la función dbo.GetNums con agregado

Ahora, si acumula los tiempos de ejecución de los operadores individuales, obtendrá un número similar al tiempo total de ejecución del plan.

La Figura 9 tiene una comparación de rendimiento en términos de tiempo transcurrido entre las tres soluciones que utilizan tanto la asignación de variables como las técnicas de prueba agregada.

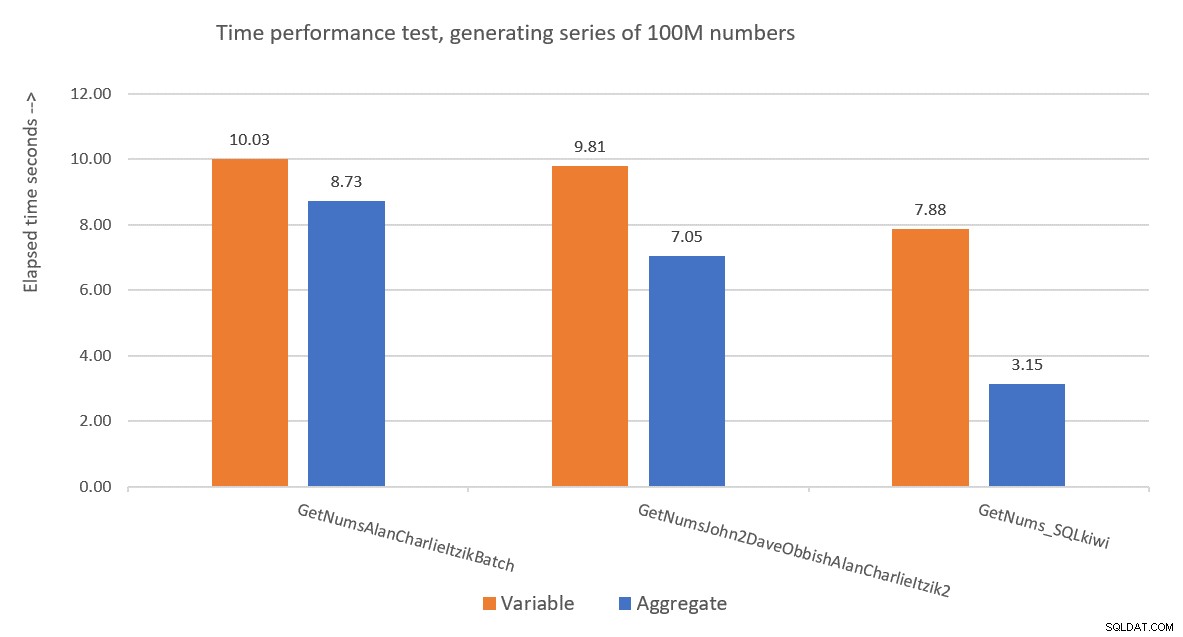Figura 9:Comparación de rendimiento

La solución de Paul es claramente ganadora, y esto es especialmente evidente cuando se usa la técnica de prueba agregada. ¡Qué hazaña tan impresionante!

Deconstruyendo y reconstruyendo la solución de Paul

Deconstruir y luego reconstruir la solución de Paul es un gran ejercicio, y aprendes mucho mientras lo haces. Como se sugirió anteriormente, le recomiendo que realice el proceso usted mismo antes de continuar leyendo.

La primera elección que debe hacer es la técnica que usaría para generar el número potencial deseado de filas de 4B. Paul optó por usar una tabla de almacén de columnas y llenarla con tantas filas como la raíz cuadrada del número requerido, lo que significa 65 536 filas, de modo que con una única unión cruzada, se obtenga el número requerido. Tal vez esté pensando que con menos de 102 400 filas no obtendrá un grupo de filas comprimido, pero esto se aplica cuando completa la tabla con una declaración INSERT como hicimos con la tabla dbo.NullBits102400. No se aplica cuando crea un índice de almacén de columnas en una tabla rellenada previamente. Así que Paul usó una instrucción SELECT INTO para crear y completar la tabla como un montón basado en un almacén de filas con 65 536 filas y luego creó un índice de almacén de columnas agrupado, lo que resultó en un grupo de filas comprimido.

El próximo desafío es descubrir cómo hacer que una combinación cruzada se procese con un operador de modo por lotes. Para esto, necesita que el algoritmo de unión sea hash. Recuerde que una unión cruzada se optimiza utilizando el algoritmo de bucles anidados. De alguna manera, debe engañar al optimizador para que piense que está utilizando una unión igualitaria interna (el hash requiere al menos un predicado basado en la igualdad), pero obtenga una unión cruzada en la práctica.

Un primer intento obvio es usar una unión interna con un predicado de unión artificial que siempre sea verdadero, así:

SELECT *
FROM dbo.CS AS N1
  INNER HASH JOIN dbo.CS AS N2
    ON 0 = 0;

Pero este código falla con el siguiente error:

El optimizador de SQL Server reconoce que se trata de un predicado de combinación interna artificial, simplifica la combinación interna a una combinación cruzada y produce un error que dice que no puede acomodar la sugerencia para forzar un algoritmo de combinación hash.

Para resolver esto, Paul creó una columna INT NOT NULL (más sobre por qué esta especificación en breve) llamada n1 en su tabla dbo.CS y la completó con 0 en todas las filas. Luego usó el predicado de combinación N2.n1 =N1.n1, obteniendo de manera efectiva la proposición 0 =0 en todas las evaluaciones de coincidencias, mientras cumplía con los requisitos mínimos para un algoritmo de combinación hash.

Esto funciona y produce un plan de modo por lotes:

SELECT *
FROM dbo.CS AS N1
  INNER HASH JOIN dbo.CS AS N2
    ON N2.n1 = N1.n1;

En cuanto a la razón por la que n1 se define como INT NOT NULL; ¿Por qué no permitir NULL y por qué no usar BIGINT? El motivo de estas opciones es evitar un residual de sondeo hash (un filtro adicional que aplica el operador de combinación hash más allá del predicado de combinación original), lo que podría generar un costo adicional innecesario. Consulte el artículo de Paul Rendimiento de unión, conversiones implícitas y residuos para obtener más información. Aquí está la parte del artículo que es relevante para nosotros:

Tenga en cuenta que esta optimización no se aplica a las columnas bigint".

Para verificar este aspecto, creemos otra tabla llamada dbo.CS2 con una columna n1 anulable:

DROP TABLE IF EXISTS dbo.CS2;
 
SELECT * INTO dbo.CS2 FROM dbo.CS;
 
ALTER TABLE dbo.CS2 ALTER COLUMN n1 INT NULL;
 
CREATE CLUSTERED COLUMNSTORE INDEX CCI 
ON dbo.CS2
WITH (MAXDOP = 1);

Primero probemos una consulta contra dbo.CS (donde n1 se define como INT NOT NULL), generando números de fila base 4B en una columna llamada rn y aplicando el agregado MAX a la columna:

SELECT
    mx = MAX(N.rn)
FROM
(
    SELECT 
        rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
    FROM dbo.CS AS N1
    JOIN dbo.CS AS N2
        ON N2.n1 = N1.n1
) AS N;

Compararemos el plan para esta consulta con el plan para una consulta similar contra dbo.CS2 (donde n1 se define como INT NULL):

SELECT
    mx = MAX(N.rn)
FROM
(
    SELECT 
        rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
    FROM dbo.CS2 AS N1
    JOIN dbo.CS2 AS N2
        ON N2.n1 = N1.n1
) AS N;

Los planes para ambas consultas se muestran en la Figura 10.

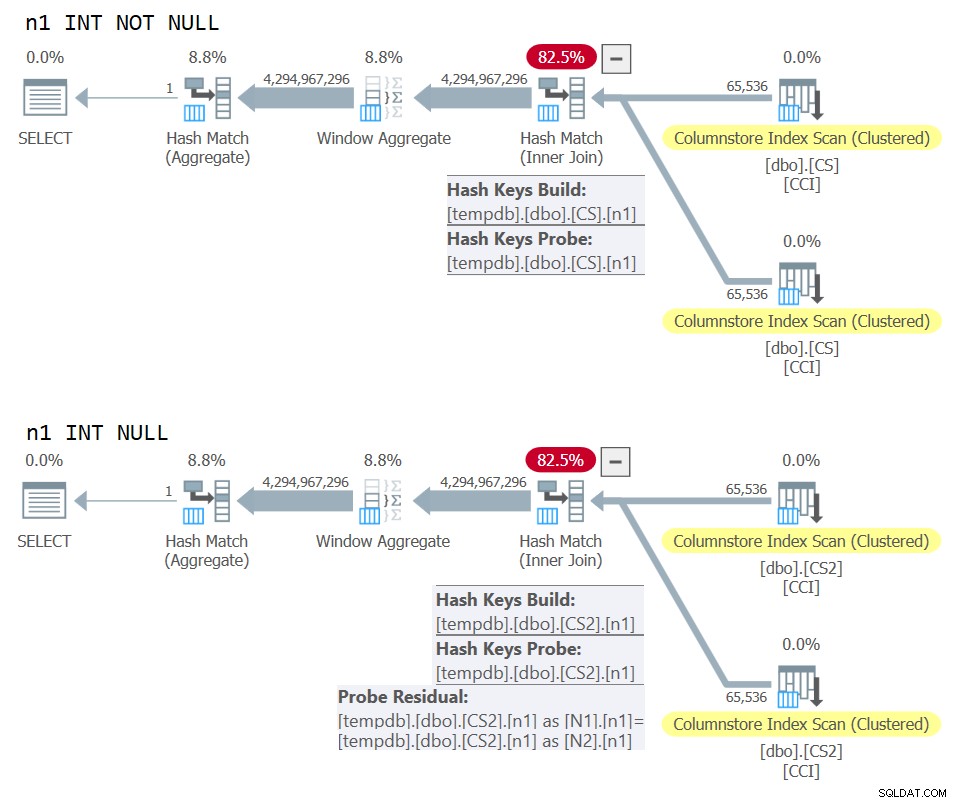Figura 10:Comparación de planes para clave de unión NOT NULL vs NULL

Puede ver claramente el residuo de sonda adicional que se aplica en el segundo plan pero no en el primero.

En mi máquina, la consulta contra dbo.CS se completó en 91 segundos y la consulta contra dbo.CS2 se completó en 92 segundos. En el artículo de Paul, informa una diferencia del 11 % a favor del caso NOT NULL para el ejemplo que usó.

Por cierto, aquellos de ustedes con buen ojo habrán notado el uso de ORDER BY @@TRANCOUNT como la especificación de pedido de la función ROW_NUMBER. Si lee atentamente los comentarios en línea de Paul en su solución, menciona que el uso de la función @@TRANCOUNT es un inhibidor de paralelismo, mientras que el uso de @@SPID no lo es. Por lo tanto, puede usar @@TRANCOUNT como la constante de tiempo de ejecución en la especificación de pedido cuando desee forzar un plan en serie y @@SPID cuando no lo desee.

Como se mencionó, la consulta contra dbo.CS tardó 91 segundos en ejecutarse en mi máquina. En este punto, podría ser interesante probar el mismo código con una verdadera combinación cruzada, permitiendo que el optimizador use un algoritmo de combinación de bucles anidados en modo fila:

SELECT
    mx = MAX(N.rn)
FROM
(
    SELECT 
        rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
    FROM dbo.CS AS N1
    CROSS JOIN dbo.CS AS N2
) AS N;

Este código tardó 104 segundos en completarse en mi máquina. Por lo tanto, obtenemos una mejora considerable del rendimiento con la unión hash en modo por lotes.

Nuestro próximo problema es el hecho de que al usar TOP para filtrar el número deseado de filas, se obtiene un plan con un operador Top en modo fila. Aquí hay un intento de implementar la función dbo.GetNums_SQLkiwi con un filtro TOP:

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT TOP (100000000 - 1 + 1)
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            ON N2.n1 = N1.n1
        ORDER BY rn
    ) AS N;
GO

Probemos la función:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

Obtuve el plan que se muestra en la Figura 11 para esta prueba.

Figura 11:Plan con filtro TOP

Observe que el operador Superior es el único en el plan que utiliza el procesamiento en modo fila.

Obtuve las siguientes estadísticas de tiempo para esta ejecución:

La mayor parte del tiempo de ejecución de este plan lo dedica el operador superior de modo de fila y el hecho de que el plan debe pasar por la conversión de modo de lote a fila y viceversa.

Nuestro desafío es descubrir una alternativa de filtrado en modo por lotes al TOP en modo fila. Los filtros basados ​​en predicados como los que se aplican con la cláusula WHERE pueden manejarse potencialmente con el procesamiento por lotes.

El enfoque de Paul fue introducir una segunda columna de tipo INT (vea el comentario en línea “todo está normalizado a 64 bits en el modo de lote/almacén de columnas de todos modos” ) llamó a n2 a la tabla dbo.CS y la rellenó con la secuencia de enteros del 1 al 65.536. En el código de la solución, utilizó dos filtros basados ​​en predicados. Uno es un filtro grueso en la consulta interna con predicados que involucran la columna n2 de ambos lados de la combinación. Este filtro grueso puede dar como resultado algunos falsos positivos. Aquí está el primer intento simplista de dicho filtro:

WHERE
    -- Coarse filter:
    N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
    AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))

Con las entradas 1 y 100,000,000 como @low y @high, no obtiene falsos positivos. Pero intente con 1 y 100,000,001, y obtendrá algunos. Obtendrá una secuencia de 100 020 001 números en lugar de 100 000 001.

Para eliminar los falsos positivos, Paul agregó un segundo filtro preciso que involucra la columna rn en la consulta externa. Aquí está el primer intento simplista de un filtro tan preciso:

WHERE
    -- Precise filter:
    N.rn < @high - @low + 2

Revisemos la definición de la función para usar los filtros basados ​​en predicados anteriores en lugar de TOP, toma 1:

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT
            rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            ON N2.n1 = N1.n1
        WHERE
            -- Coarse filter:
            N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
    ) AS N
    WHERE
        -- Precise filter:
        N.rn < @high - @low + 2;
GO

Probemos la función:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

Obtuve el plan que se muestra en la Figura 12 para esta prueba.

Figura 12:Plan con filtro WHERE, toma 1

Por desgracia, algo claramente salió mal. SQL Server convirtió nuestro filtro basado en predicados que involucraba la columna rn en un filtro basado en TOP y lo optimizó con un operador Top, que es exactamente lo que intentamos evitar. Para colmo de males, el optimizador también decidió utilizar el algoritmo de bucles anidados para la unión.

Este código tardó 18,8 segundos en terminar en mi máquina. No se ve bien.

Con respecto a la combinación de bucles anidados, esto es algo que podríamos solucionar fácilmente usando una sugerencia de combinación en la consulta interna. Solo para ver el impacto en el rendimiento, aquí hay una prueba con una sugerencia de consulta de combinación hash forzada utilizada en la consulta de prueba:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(HASH JOIN);

El tiempo de ejecución se reduce a 13,2 segundos.

Todavía tenemos el problema con la conversión del filtro WHERE contra rn a un filtro TOP. Tratemos de entender cómo sucedió esto. Usamos el siguiente filtro en la consulta externa:

WHERE N.rn < @high - @low + 2

Recuerde que rn representa una expresión basada en ROW_NUMBER no manipulada. Un filtro basado en una expresión no manipulada de este tipo que se encuentra en un rango determinado a menudo se optimiza con un operador Top, lo que para nosotros es una mala noticia debido al uso del procesamiento en modo fila.

La solución alternativa de Paul fue usar un predicado equivalente, pero uno que aplicara manipulación a rn, así:

WHERE @low - 2 + N.rn < @high

Filtrar una expresión que agrega manipulación a una expresión basada en ROW_NUMBER inhibe la conversión del filtro basado en predicado a uno basado en TOP. ¡Eso es genial!

Let’s revise the function’s definition to use the above WHERE predicate, take 2:

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT
            rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            ON N2.n1 = N1.n1
        WHERE
            -- Coarse filter:
            N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
    ) AS N
    WHERE
        -- Precise filter:
        @low - 2 + N.rn < @high;
GO

Test the function again, without any special hints or anything:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

It naturally gets an all-batch-mode plan with a hash join algorithm and no Top operator, resulting in an execution time of 3.177 seconds. Looking good.

The next step is to check if the solution handles bad inputs well. Let’s try it with a negative delta:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(100000000, 1);

This execution fails with the following error.

Paul’s solution involved two additions. One is to add the following predicate to the inner query’s WHERE clause:

 @high >= @low

This filter does more than what it seems initially. If you’ve read Paul’s inline comments carefully, you could find this part:

The intriguing part here is the potential to use a constant scan with constants as inputs. I’ll get to this shortly.

The other addition is to apply the IIF function to the input expression to the SQRT function. This is done to avoid negative input when using nonconstants as inputs to our numbers function, and in case the optimizer decides to handle the predicate involving SQRT before the predicate @high>=@low.

Before the IIF addition, for example, the predicate involving N1.n2 looked like this:

N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))

After adding IIF, it looks like this:

N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))

With these two additions, we’re now basically ready for the final definition of the dbo.GetNums_SQLkiwi function:

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT 
            -- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            -- Batch mode hash cross join
            -- Integer not null data type avoid hash probe residual
            -- This is always 0 = 0
            ON N2.n1 = N1.n1
        WHERE
            -- Try to avoid SQRT on negative numbers and enable simplification 
            -- to single constant scan if @low > @high (with literals)
            -- No start-up filters in batch mode
            @high >= @low
            -- Coarse filter:
            -- Limit each side of the cross join to SQRT(target number of rows)
            -- IIF avoids SQRT on negative numbers with parameters
            AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
    ) AS N
    WHERE
        -- Precise filter:
        -- Batch mode filter the limited cross join to the exact number of rows needed
        -- Avoids the optimizer introducing a row-mode Top with following row mode compute scalar
        @low - 2 + N.rn < @high;
GO

Now back to the comment about the constant scan. When using constants that result in a negative range as inputs to the function, e.g., 100,000,000 and 1 as @low and @high, after parameter embedding the WHERE filter of the inner query looks like this:

WHERE
    1 >= 100000000
    AND ...

The whole plan can then be simplified to a single Constant Scan operator. Pruébalo:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(100000000, 1);

The plan for this execution is shown in Figure 13.

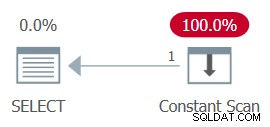Figure 13:Plan with constant scan

Unsurprisingly, I got the following performance numbers for this execution:

logical reads 0

When passing a negative range with nonconstants as inputs, the use of the IIF function will prevent any attempt to compute a square root of a negative input.

Now let’s test the function with a valid input range:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

You get the all-batch-mode plan shown in Figure 14.

Figure 14:Plan for dbo.GetNums_SQLkiwi function

This is the same plan you saw earlier in Figure 7.

I got the following time statistics for this execution:

Ladies and gentlemen, I think we have a winner! :)

Conclusión

I’ll have what Paul’s having.

Are we done yet, or is this series going to last forever?

No and no.