Cuando SQL Server optimiza una consulta, durante una fase de exploración produce planes candidatos y elige entre ellos el que tiene el costo más bajo. Se supone que el plan elegido tiene el tiempo de ejecución más bajo entre los planes explorados. La cuestión es que el optimizador solo puede elegir entre estrategias que fueron codificadas en él. Por ejemplo, al optimizar la agrupación y la agregación, a la fecha de este escrito, el optimizador solo puede elegir entre las estrategias Stream Aggregate y Hash Aggregate. Cubrí las estrategias disponibles en partes anteriores de esta serie. En la Parte 1, cubrí la estrategia de Agregado de flujo preordenado, en la Parte 2, la estrategia Ordenar + Agregado de flujo, en la Parte 3, la estrategia Agregado de hash y en la Parte 4, consideraciones de paralelismo.
Lo que el optimizador de SQL Server actualmente no admite es la personalización y la inteligencia artificial. Es decir, si puede descubrir una estrategia que, en determinadas condiciones, es más óptima que las que admite el optimizador, no puede mejorar el optimizador para que la admita y el optimizador no puede aprender a usarlo. Sin embargo, lo que puede hacer es reescribir la consulta utilizando elementos de consulta alternativos que pueden optimizarse con la estrategia que tiene en mente. En esta quinta y última parte de la serie, demuestro esta técnica de ajuste de consultas mediante revisiones de consultas.
¡Muchas gracias a Paul White (@SQL_Kiwi) por ayudar con algunos de los cálculos de costos presentados en este artículo!
Al igual que en las partes anteriores de la serie, usaré la base de datos de muestra PerformanceV3. Utilice el siguiente código para eliminar índices innecesarios de la tabla Pedidos:
DROP INDEX idx_nc_sid_od_cid ON dbo.Orders; DROP INDEX idx_unc_od_oid_i_cid_eid ON dbo.Orders;
Estrategia de optimización predeterminada
Considere las siguientes tareas básicas de agrupación y agregación:
Devuelve la fecha máxima de pedido para cada remitente, empleado y cliente.
Para un rendimiento óptimo, cree los siguientes índices de soporte:
CREATE INDEX idx_sid_od ON dbo.Orders(shipperid, orderdate); CREATE INDEX idx_eid_od ON dbo.Orders(empid, orderdate); CREATE INDEX idx_cid_od ON dbo.Orders(custid, orderdate);
Las siguientes son las tres consultas que usaría para manejar estas tareas, junto con los costos estimados del subárbol, así como las estadísticas de E/S, CPU y tiempo transcurrido:
-- Query 1 -- Estimated Subtree Cost: 3.5344 -- logical reads: 2484, CPU time: 281 ms, elapsed time: 279 ms SELECT shipperid, MAX(orderdate) AS maxod FROM dbo.Orders GROUP BY shipperid; -- Query 2 -- Estimated Subtree Cost: 3.62798 -- logical reads: 2610, CPU time: 250 ms, elapsed time: 283 ms SELECT empid, MAX(orderdate) AS maxod FROM dbo.Orders GROUP BY empid; -- Query 3 -- Estimated Subtree Cost: 4.27624 -- logical reads: 3479, CPU time: 406 ms, elapsed time: 506 ms SELECT custid, MAX(orderdate) AS maxod FROM dbo.Orders GROUP BY custid;
La Figura 1 muestra los planes para estas consultas:
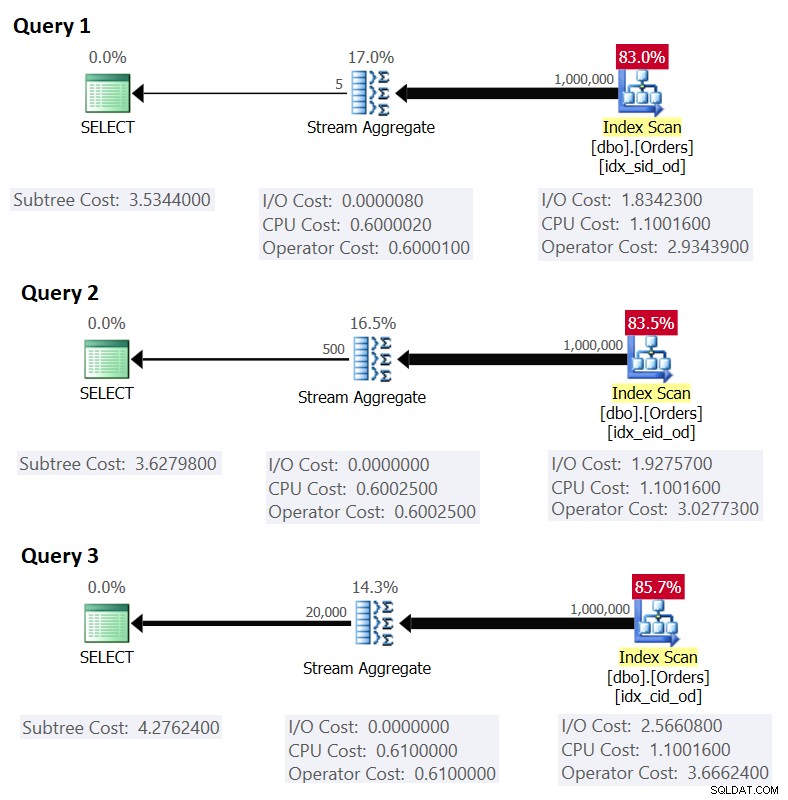Figura 1:Planes para consultas agrupadas
Recuerde que si tiene un índice de cobertura en su lugar, con las columnas del conjunto de agrupaciones como columnas clave principales, seguidas de la columna de agregación, es probable que SQL Server elija un plan que realice una exploración ordenada del índice de cobertura compatible con la estrategia Stream Aggregate. . Como es evidente en los planes de la Figura 1, el operador de Index Scan es responsable de la mayor parte del costo del plan, y dentro de él, la parte de E/S es la más destacada.
Antes de presentar una estrategia alternativa y explicar las circunstancias bajo las cuales es más óptima que la estrategia predeterminada, evalúemos el costo de la estrategia existente. Dado que la parte de E/S es la más dominante para determinar el costo del plan de esta estrategia predeterminada, primero estimemos cuántas lecturas de páginas lógicas se requerirán. Más adelante también estimaremos el costo del plan.
Para estimar la cantidad de lecturas lógicas que requerirá el operador Index Scan, debe saber cuántas filas tiene en la tabla y cuántas filas caben en una página según el tamaño de fila. Una vez que tenga estos dos operandos, su fórmula para el número requerido de páginas en el nivel de hoja del índice es TECHO (1e0 * @numrows / @rowsperpage). Si todo lo que tiene es solo la estructura de la tabla y no hay datos de muestra existentes con los que trabajar, puede usar este artículo para estimar la cantidad de páginas que tendría en el nivel de hoja del índice de soporte. Si tiene buenos datos de muestra representativos, incluso si no están en la misma escala que en el entorno de producción, puede calcular el número promedio de filas que caben en una página consultando el catálogo y los objetos de administración dinámica, así:
SELECT I.name, row_count, in_row_data_page_count,
CAST(ROUND(1e0 * row_count / in_row_data_page_count, 0) AS INT) AS avgrowsperpage
FROM sys.indexes AS I
INNER JOIN sys.dm_db_partition_stats AS P
ON I.object_id = P.object_id
AND I.index_id = P.index_id
WHERE I.object_id = OBJECT_ID('dbo.Orders')
AND I.name IN ('idx_sid_od', 'idx_eid_od', 'idx_cid_od'); Esta consulta genera el siguiente resultado en nuestra base de datos de ejemplo:
name row_count in_row_data_page_count avgrowsperpage ----------- ---------- ---------------------- --------------- idx_sid_od 1000000 2473 404 idx_eid_od 1000000 2599 385 idx_cid_od 1000000 3461 289
Ahora que tiene el número de filas que caben en una página hoja del índice, puede estimar el número total de páginas hoja en el índice en función del número de filas que espera que tenga su tabla de producción. Este también será el número esperado de lecturas lógicas que aplicará el operador de Index Scan. En la práctica, hay más en la cantidad de lecturas que podrían tener lugar que solo la cantidad de páginas en el nivel de hoja del índice, como lecturas adicionales producidas por el mecanismo de lectura anticipada, pero las ignoraré para simplificar nuestra discusión. .
Por ejemplo, la cantidad estimada de lecturas lógicas para la Consulta 1 con respecto a la cantidad esperada de filas es TECHO (1e0 * @numorws / 404). Con 1 000 000 de filas, el número esperado de lecturas lógicas es 2476. La diferencia entre 2476 y el recuento de páginas en fila informado de 2473 se puede atribuir al redondeo que hice al calcular el número promedio de filas por página.
En cuanto al costo del plan, expliqué cómo aplicar ingeniería inversa al costo del operador de Stream Aggregate en la Parte 1 de la serie. De manera similar, puede aplicar ingeniería inversa al costo del operador de Index Scan. El costo del plan es entonces la suma de los costos de los operadores Index Scan y Stream Aggregate.
Para calcular el costo del operador Index Scan, desea comenzar con la ingeniería inversa de algunas de las constantes importantes del modelo de costos:
@randomio = 0.003125 -- Random I/O cost @seqio = 0.000740740740741 -- Sequential I/O cost @cpubase = 0.000157 -- CPU base cost @cpurow = 0.0000011 -- CPU cost per row
Con las constantes del modelo de costos anteriores resueltas, puede proceder a la ingeniería inversa de las fórmulas para el costo de E/S, el costo de la CPU y el costo total del operador para el operador Index Scan:
I/O cost: @randomio + (@numpages - 1e0) * @seqio = 0.003125 + (@numpages - 1e0) * 0.000740740740741 CPU cost: @cpubase + @numrows * @cpurow = 0.000157 + @numrows * 0.0000011 Operator cost: 0.002541259259259 + @numpages * 0.000740740740741 + @numrows * 0.0000011
Por ejemplo, el costo del operador de Index Scan para la Consulta 1, con 2473 páginas y 1,000,000 de filas, es:
0.002541259259259 + 2473 * 0.000740740740741 + 1000000 * 0.0000011 = 2.93439
La siguiente es la fórmula de ingeniería inversa para el costo del operador de Stream Aggregate:
0.000008 + @numrows * 0.0000006 + @numgroups * 0.0000005
Como ejemplo, para la Consulta 1, tenemos 1 000 000 de filas y 5 grupos, por lo que el costo estimado es 0,6000105.
Combinando los costos de los dos operadores, esta es la fórmula para el costo total del plan:
0.002549259259259 + @numpages * 0.000740740740741 + @numrows * 0.0000017 + @numgroups * 0.0000005
Para la Consulta 1, con 2473 páginas, 1 000 000 de filas y 5 grupos, obtiene:
0.002549259259259 + 2473 * 0.000740740740741 + 1000000 * 0.0000017 + 5 * 0.0000005 = 3.5344
Esto coincide con lo que muestra la Figura 1 como el costo estimado para la Consulta 1.
Si confiara en un número estimado de filas por página, su fórmula sería:
0.002549259259259 + CEILING(1e0 * @numrows / @rowsperpage) * 0.000740740740741 + @numrows * 0.0000017 + @numgroups * 0.0000005
Como ejemplo, para la Consulta 1, con 1 000 000 de filas, 404 filas por página y 5 grupos, el costo estimado es:
0.002549259259259 + CEILING(1e0 * 1000000 / 404) * 0.000740740740741 + 1000000 * 0.0000017 + 5 * 0.0000005 = 3.5366
Como ejercicio, puede aplicar los números para la Consulta 2 (1 000 000 filas, 385 filas por página, 500 grupos) y la Consulta 3 (1 000 000 filas, 289 filas por página, 20 000 grupos) en nuestra fórmula y ver que los resultados coinciden con lo que La figura 1 muestra.
Ajuste de consultas con reescrituras de consultas
La estrategia preordenada predeterminada de Stream Aggregate para calcular un agregado MIN/MAX por grupo se basa en un escaneo ordenado de un índice de cobertura de soporte (o alguna otra actividad preliminar que emite las filas ordenadas). Una estrategia alternativa, con un índice de cobertura de apoyo presente, sería realizar una búsqueda de índice por grupo. Aquí hay una descripción de un pseudo plan basado en una estrategia de este tipo para una consulta que agrupa por grpcol y aplica un MAX(aggcol):
set @curgrpcol = grpcol from first row obtained by a scan of the index, ordered forward;
while end of index not reached
begin
set @curagg = aggcol from row obtained by a seek to the last point
where grpcol = @curgrpcol, ordered backward;
emit row (@curgrpcol, @curagg);
set @curgrpcol = grpcol from row to the right of last row for current group;
end; Si lo piensa, la estrategia predeterminada basada en escaneo es óptima cuando el conjunto de agrupación tiene baja densidad (gran cantidad de grupos, con una pequeña cantidad de filas por grupo en promedio). La estrategia basada en búsquedas es óptima cuando el conjunto de agrupación tiene una alta densidad (pequeño número de grupos, con un gran número de filas por grupo en promedio). La figura 2 ilustra ambas estrategias y muestra cuándo cada una es óptima.
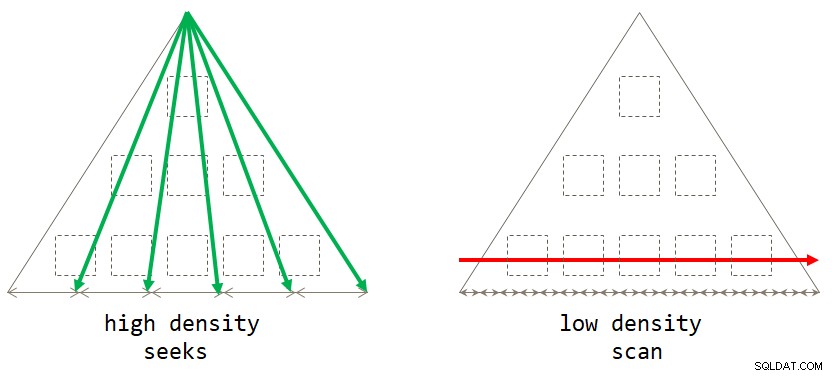Figura 2:estrategia óptima basado en la densidad del conjunto de agrupación
Siempre que escriba la solución en forma de una consulta agrupada, actualmente SQL Server solo considerará la estrategia de exploración. Esto funcionará bien para usted cuando el conjunto de agrupación tenga baja densidad. Cuando tiene alta densidad, para obtener la estrategia de búsqueda, deberá aplicar una reescritura de consulta. Una forma de lograr esto es consultar la tabla que contiene los grupos y utilizar una subconsulta agregada escalar en la tabla principal para obtener el agregado. Por ejemplo, para calcular la fecha máxima de pedido para cada remitente, usaría el siguiente código:
SELECT shipperid,
( SELECT TOP (1) O.orderdate
FROM dbo.Orders AS O
WHERE O.shipperid = S.shipperid
ORDER BY O.orderdate DESC ) AS maxod
FROM dbo.Shippers AS S; Las pautas de indexación para la tabla principal son las mismas que las que respaldan la estrategia predeterminada. Ya contamos con esos índices para las tres tareas antes mencionadas. Probablemente también desee un índice de apoyo en las columnas del conjunto de agrupación en la tabla que contiene los grupos para minimizar el costo de E/S en esa tabla. Utilice el siguiente código para crear dichos índices de apoyo para nuestras tres tareas:
CREATE INDEX idx_sid ON dbo.Shippers(shipperid); CREATE INDEX idx_eid ON dbo.Employees(empid); CREATE INDEX idx_cid ON dbo.Customers(custid);
Sin embargo, un pequeño problema es que la solución basada en la subconsulta no es un equivalente lógico exacto de la solución basada en la consulta agrupada. Si tiene un grupo sin presencia en la tabla principal, el primero devolverá el grupo con un NULL como agregado, mientras que el último no devolverá el grupo en absoluto. Una forma sencilla de lograr un verdadero equivalente lógico a la consulta agrupada es invocar la subconsulta usando el operador CROSS APPLY en la cláusula FROM en lugar de usar una subconsulta escalar en la cláusula SELECT. Recuerde que CROSS APPLY no devolverá una fila izquierda si la consulta aplicada devuelve un conjunto vacío. Estas son las tres consultas de solución que implementan esta estrategia para nuestras tres tareas, junto con sus estadísticas de rendimiento:
-- Query 4
-- Estimated Subtree Cost: 0.0072299
-- logical reads: 2 + 15, CPU time: 0 ms, elapsed time: 43 ms
SELECT S.shipperid, A.orderdate AS maxod
FROM dbo.Shippers AS S
CROSS APPLY ( SELECT TOP (1) O.orderdate
FROM dbo.Orders AS O
WHERE O.shipperid = S.shipperid
ORDER BY O.orderdate DESC ) AS A;
-- Query 5
-- Estimated Subtree Cost: 0.089694
-- logical reads: 2 + 1620, CPU time: 0 ms, elapsed time: 148 ms
SELECT E.empid, A.orderdate AS maxod
FROM dbo.Employees AS E
CROSS APPLY ( SELECT TOP (1) O.orderdate
FROM dbo.Orders AS O
WHERE O.empid = E.empid
ORDER BY O.orderdate DESC ) AS A;
-- Query 6
-- Estimated Subtree Cost: 3.5227
-- logical reads: 45 + 63777, CPU time: 171 ms, elapsed time: 306 ms
SELECT C.custid, A.orderdate AS maxod
FROM dbo.Customers AS C
CROSS APPLY ( SELECT TOP (1) O.orderdate
FROM dbo.Orders AS O
WHERE O.custid = C.custid
ORDER BY O.orderdate DESC ) AS A; Los planes para estas consultas se muestran en la Figura 3.
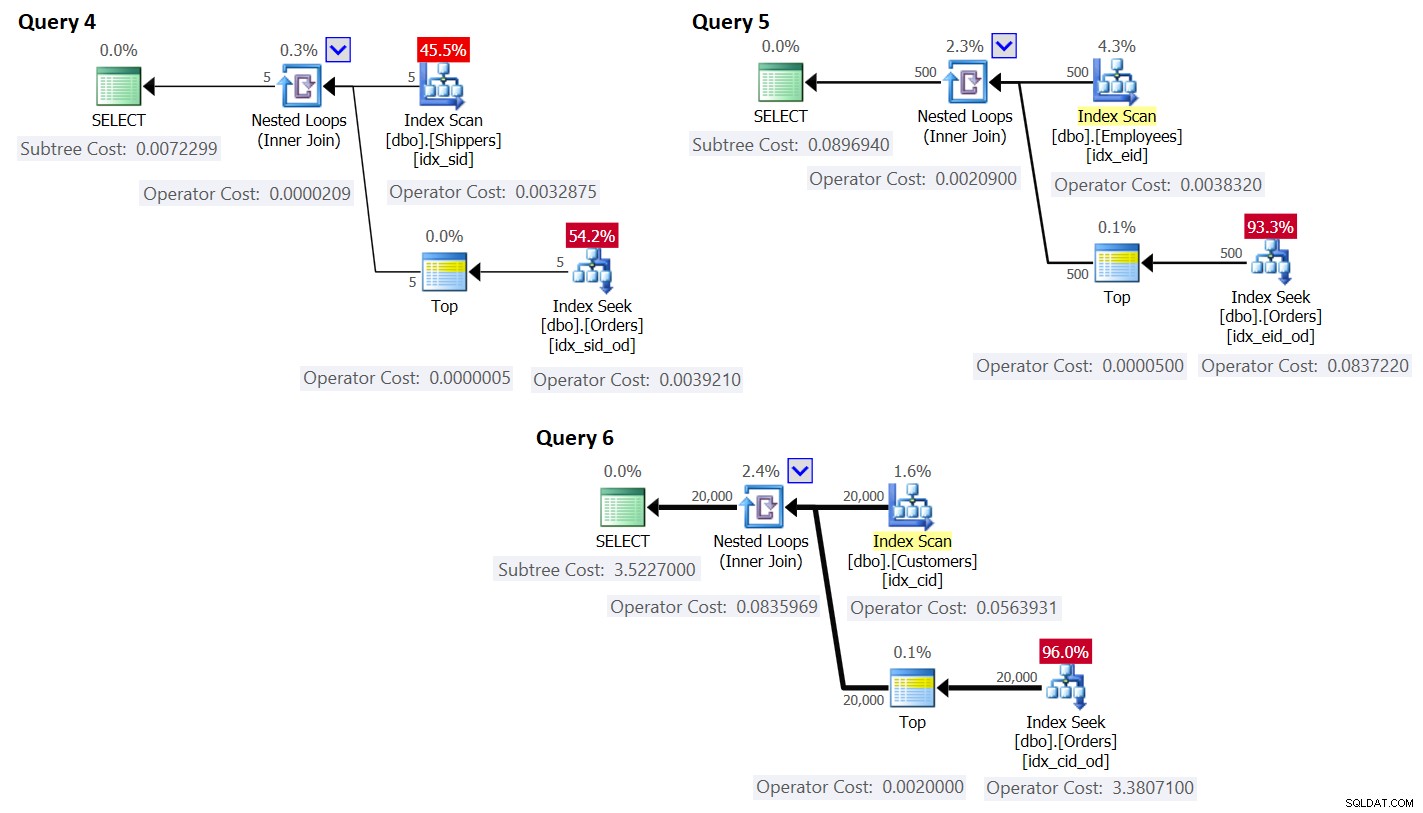Figura 3:Planes para consultas con reescritura
Como puede ver, los grupos se obtienen escaneando el índice en la tabla de grupos, y el agregado se obtiene aplicando una búsqueda en el índice de la tabla principal. Cuanto mayor sea la densidad del conjunto de agrupación, más óptimo será este plan en comparación con la estrategia predeterminada para la consulta agrupada.
Al igual que hicimos anteriormente para la estrategia de escaneo predeterminada, calculemos la cantidad de lecturas lógicas y el costo del plan para la estrategia de búsqueda. El número estimado de lecturas lógicas es el número de lecturas para la ejecución única del operador Index Scan que recupera los grupos, más las lecturas para todas las ejecuciones del operador Index Seek.
El número estimado de lecturas lógicas para el operador Index Scan es insignificante en comparación con las búsquedas; aún así, es TECHO (1e0 * @numgroups / @rowsperpage). Tome la consulta 4 como ejemplo; digamos que el índice idx_sid se ajusta a unas 600 filas por página hoja (el número real depende de los valores reales de shipperid ya que el tipo de datos es VARCHAR(5)). Con 5 grupos, todas las filas caben en una página de una sola hoja. Si tuviera 5000 grupos, cabrían en 9 páginas.
El número estimado de lecturas lógicas para todas las ejecuciones del operador Index Seek es @numgroups * @index depth. La profundidad del índice se puede calcular como:
CEILING(LOG(CEILING(1e0 * @numrows / @rowsperleafpage), @rowspernonleafpage)) + 1
Usando la consulta 4 como ejemplo, digamos que podemos ajustar alrededor de 404 filas por página de hoja del índice idx_sid_od y alrededor de 352 filas por página sin hoja. Una vez más, los números reales dependerán de los valores reales almacenados en la columna shipperid ya que su tipo de datos es VARCHAR(5)). Para estimaciones, recuerde que puede utilizar los cálculos descritos aquí. Con buenos datos de muestra representativos disponibles, puede usar la siguiente consulta para calcular la cantidad de filas que pueden caber en las páginas hoja y no hoja del índice dado:
SELECT
CASE P.index_level WHEN 0 THEN 'leaf' WHEN 1 THEN 'nonleaf' END AS pagetype,
FLOOR(8096 / (P.avg_record_size_in_bytes + 2)) AS rowsperpage
FROM (SELECT *
FROM sys.indexes
WHERE object_id = OBJECT_ID('dbo.Orders')
AND name = 'idx_sid_od') AS I
CROSS APPLY sys.dm_db_index_physical_stats
(DB_ID('PerformanceV3'), I.object_id, I.index_id, NULL, 'DETAILED') AS P
WHERE P.index_level <= 1; Obtuve el siguiente resultado:
pagetype rowsperpage -------- ---------------------- leaf 404 nonleaf 352
Con estos números, la profundidad del índice con respecto al número de filas de la tabla es:
CEILING(LOG(CEILING(1e0 * @numrows / 404), 352)) + 1
Con 1 000 000 de filas en la tabla, esto da como resultado una profundidad de índice de 3. Con alrededor de 50 millones de filas, la profundidad del índice aumenta a 4 niveles, y con alrededor de 17 620 millones de filas aumenta a 5 niveles.
En cualquier caso, con respecto al número de grupos y el número de filas, suponiendo el número anterior de filas por página, la siguiente fórmula calcula el número estimado de lecturas lógicas para la Consulta 4:
CEILING(1e0 * @numgroups / 600) + @numgroups * (CEILING(LOG(CEILING(1e0 * @numrows / 404), 352)) + 1)
Por ejemplo, con 5 grupos y 1 000 000 de filas, ¡obtienes solo 16 lecturas en total! Recuerde que la estrategia predeterminada basada en exploración para la consulta agrupada implica tantas lecturas lógicas como CEILING(1e0 * @numrows / @rowsperpage). Utilizando la Consulta 1 como ejemplo, y suponiendo unas 404 filas por página hoja del índice idx_sid_od, con el mismo número de filas de 1 000 000, obtendrá unas 2476 lecturas. Aumente el número de filas en la tabla por un factor de 1,000 a 1,000,000,000, pero mantenga fijo el número de grupos. La cantidad de lecturas requeridas con la estrategia de búsqueda cambia muy poco a 21, mientras que la cantidad de lecturas requeridas con la estrategia de escaneo aumenta linealmente a 2,475,248.
La belleza de la estrategia de búsqueda es que mientras el número de grupos sea pequeño y fijo, tiene una escala casi constante con respecto al número de filas en la tabla. Esto se debe a que la cantidad de búsquedas está determinada por la cantidad de grupos, y la profundidad del índice se relaciona con la cantidad de filas en la tabla de forma logarítmica, donde la base logarítmica es la cantidad de filas que caben en una página sin hojas. Por el contrario, la estrategia basada en escaneo tiene una escala lineal con respecto al número de filas involucradas.
La figura 4 muestra el número de lecturas estimado para las dos estrategias, aplicadas por Consulta 1 y Consulta 4, con un número fijo de grupos de 5 y diferentes números de filas en la tabla principal.
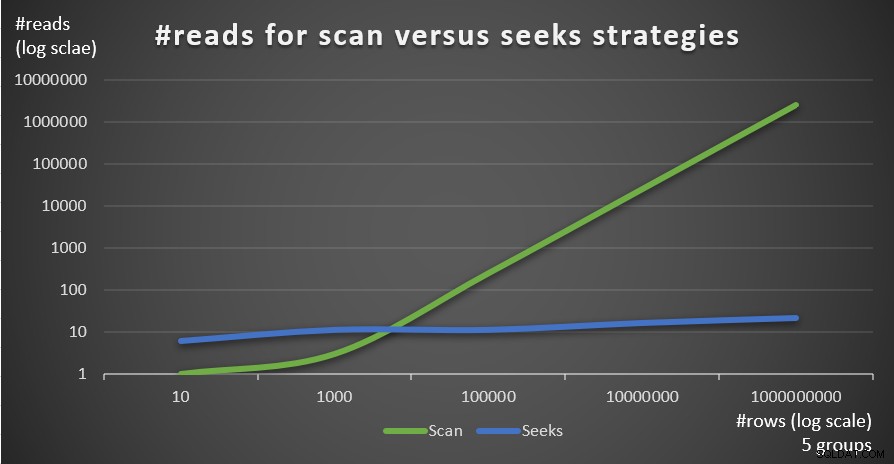Figura 4:#lecturas para estrategias de exploración frente a estrategias de búsqueda (5 grupos)
La Figura 5 muestra el número de lecturas estimado para las dos estrategias, dado un número fijo de filas de 1 000 000 en la tabla principal y diferentes números de grupos.
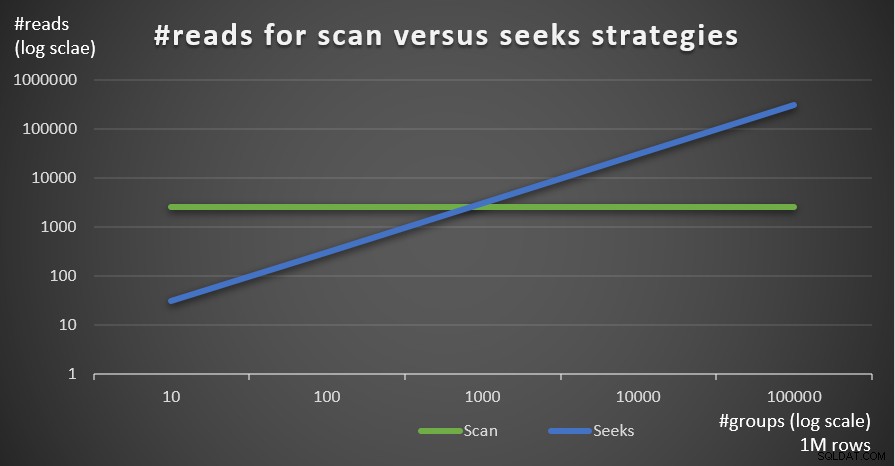Figura 5:#lecturas para estrategias de exploración frente a búsquedas (1 millón de filas)
Puede ver muy claramente que cuanto mayor sea la densidad del conjunto de agrupación (menor número de grupos) y cuanto mayor sea la tabla principal, más se prefiere la estrategia de búsqueda en términos de número de lecturas. Si se pregunta sobre el patrón de E/S utilizado por cada estrategia; claro, las operaciones de búsqueda de índice realizan E/S aleatorias, mientras que una operación de exploración de índice realiza E/S secuencial. Aún así, está bastante claro qué estrategia es más óptima en los casos más extremos.
En cuanto al costo del plan de consultas, de nuevo, usando el plan para la Consulta 4 en la Figura 3 como ejemplo, dividámoslo en operadores individuales en el plan.
La fórmula de ingeniería inversa para el costo del operador Index Scan es:
0.002541259259259 + @numpages * 0.000740740740741 + @numgroups * 0.0000011
En nuestro caso, con 5 grupos, todos los cuales caben en una página, el costo es:
0.002541259259259 + 1 * 0.000740740740741 + 5 * 0.0000011 = 0.0032875
El costo que se muestra en el plan es el mismo.
Como antes, podría estimar el número de páginas en el nivel de hoja del índice en función del número estimado de filas por página mediante la fórmula TECHO (1e0 * @numrows / @rowsperpage), que en nuestro caso es TECHO (1e0 * @ numgroups / @groupsperpage). Digamos que el índice idx_sid se ajusta a unas 600 filas por página hoja, con 5 grupos que necesitarías para leer una página. En cualquier caso, la fórmula de costeo para el operador Index Scan se convierte en:
0.002541259259259 + CEILING(1e0 * @numgroups / @groupsperpage) * 0.000740740740741 + @numgroups * 0.0000011
La fórmula de cálculo de costos de ingeniería inversa para el operador Nested Loops es:
@executions * 0.00000418
En nuestro caso, esto se traduce en:
@numgroups * 0.00000418
Para la Consulta 4, con 5 grupos, obtienes:
5 * 0.00000418 = 0.0000209
El costo que se muestra en el plan es el mismo.
La fórmula de cálculo de costos de ingeniería inversa para el operador superior es:
@executions * @toprows * 0.00000001
En nuestro caso, esto se traduce en:
@numgroups * 1 * 0.00000001
Con 5 grupos, obtienes:
5 * 0.0000001 = 0.0000005
El costo que se muestra en el plan es el mismo.
En cuanto al operador Index Seek, aquí obtuve una gran ayuda de Paul White; ¡gracias mi amigo! El cálculo es diferente para la primera ejecución y para los rebinds (ejecuciones no primeras que no reutilizan el resultado de la ejecución anterior). Como hicimos con el operador Index Scan, comencemos identificando las constantes del modelo de costos:
@randomio = 0.003125 -- Random I/O cost @seqio = 0.000740740740741 -- Sequential I/O cost @cpubase = 0.000157 -- CPU base cost @cpurow = 0.0000011 -- CPU cost per row
Para una ejecución, sin aplicar un objetivo de fila, los costos de E/S y CPU son:
I/O cost: @randomio + (@numpages - 1e0) * @seqio = 0.002384259259259 + @numpages * 0.000740740740741 CPU cost: @cpubase + @numrows * @cpurow = 0.000157 + @numrows * 0.0000011
Dado que usamos TOP (1), solo tenemos una página y una fila involucradas, por lo que los costos son:
I/O cost: 0.002384259259259 + 1 * 0.000740740740741 = 0.003125 CPU cost: 0.000157 + 1 * 0.0000011 = 0.0001581
Entonces, el costo de la primera ejecución del operador Index Seek en nuestro caso es:
@firstexecution = 0.003125 + 0.0001581 = 0.0032831
En cuanto al costo de los reenlaces, como de costumbre, está compuesto por costos de CPU y E/S. Llamémoslos @rebindcpu y @rebindio, respectivamente. Con la Consulta 4, que tiene 5 grupos, tenemos 4 reenlaces (llámelo @rebinds). El costo de @rebindcpu es la parte fácil. La fórmula es:
@rebindcpu = @rebinds * (@cpubase + @cpurow)
En nuestro caso, esto se traduce en:
@rebindcpu = 4 * (0.000157 + 0.0000011) = 0.0006324
La parte de @rebindio es un poco más compleja. Aquí, la fórmula de cálculo de costos calcula, estadísticamente, el número esperado de páginas distintas que se espera que lean los reencuadernados mediante el muestreo con reemplazo. Llamaremos a este elemento @pswr (para distintas páginas muestreadas con reemplazo). La idea es que tenemos @indexdatapages el número de páginas en el índice (en nuestro caso, 2473) y @rebinds el número de reenlaces (en nuestro caso, 4). Suponiendo que tenemos la misma probabilidad de leer cualquier página dada con cada reenlace, ¿cuántas páginas distintas se espera que lea en total? Esto es similar a tener una bolsa con 2473 bolas, y cuatro veces a ciegas sacar una bola de la bolsa y luego devolverla a la bolsa. Estadísticamente, ¿cuántas bolas distintas se espera que saque en total? La fórmula para esto, usando nuestros operandos, es:
@pswr = @indexdatapages * (1e0 - POWER((@indexdatapages - 1e0) / @indexdatapages, @rebinds))
Con nuestros números obtienes:
@pswr = 2473 * (1e0 - POWER((2473 - 1e0) / 2473, 4)) = 3.99757445099277
A continuación, calcula el número de filas y páginas que tiene en promedio por grupo:
@grouprows = @cardinality * @density @grouppages = CEILING(@indexdatapages * @density)
En nuestra Consulta 4, la cardinalidad es 1.000.000 y la densidad es 1/5 =0,2. Entonces obtienes:
@grouprows = 1000000 * 0.2 = 200000 @numpages = CEILING(2473 * 0.2) = 495
Luego calcula el costo de E/S sin filtrar (llámelo @io) como:
@io = @randomio + (@seqio * (@grouppages - 1e0))
En nuestro caso, obtienes:
@io = 0.003125 + (0.000740740740741 * (495 - 1e0)) = 0.369050925926054
Y, por último, dado que la búsqueda extrae solo una fila en cada reenlace, calcula @rebindio usando la siguiente fórmula:
@rebindio = (1e0 / @grouprows) * ((@pswr - 1e0) * @io)
En nuestro caso, obtienes:
@rebindio = (1e0 / 200000) * ((3.99757445099277 - 1e0) * 0.369050925926054) = 0.000005531288
Finalmente, el costo del operador es:
Operator cost: @firstexecution + @rebindcpu + @rebindio = 0.0032831 + 0.0006324 + 0.000005531288 = 0.003921031288
Esto es lo mismo que el costo del operador de Index Seek que se muestra en el plan para la Consulta 4.
Ahora puede agregar los costos de todos los operadores para obtener el costo completo del plan de consulta. obtienes:
Query plan cost: 0.002541259259259 + CEILING(1e0 * @numgroups / @groupsperpage)
* 0.000740740740741 + @numgroups * 0.0000011
+ @numgroups * 0.00000418
+ @numgroups * 0.00000001
+ 0.0032831 + (@numgroups - 1e0) * 0.0001581
+ (1e0 / (@numrows / @numgroups)) * (CEILING(1e0 * @numrows / @rowsperpage)
* (1e0 - POWER((CEILING(1e0 * @numrows / @rowsperpage) - 1e0)
/ CEILING(1e0 * @numrows / @rowsperpage), @numgroups - 1e0)) - 1e0)
* (0.003125 + (0.000740740740741 * (CEILING((@numrows / @rowsperpage)
* (1e0 / @numgroups)) - 1e0))) Después de la simplificación, obtiene la siguiente fórmula de cálculo de costos completa para nuestra estrategia Seeks:
0.005666259259259 + CEILING(1e0 * @numgroups / @groupsperpage)
* 0.000740740740741 + @numgroups * 0.0000011
+ @numgroups * 0.00016229
+ (1e0 / (@numrows / @numgroups)) * (CEILING(1e0 * @numrows / @rowsperpage)
* (1e0 - POWER((CEILING(1e0 * @numrows / @rowsperpage) - 1e0)
/ CEILING(1e0 * @numrows / @rowsperpage), @numgroups - 1e0)) - 1e0)
* (0.003125 + (0.000740740740741 * (CEILING((@numrows / @rowsperpage)
* (1e0 / @numgroups)) - 1e0))) Como ejemplo, usando T-SQL, aquí está el cálculo del costo del plan de consulta con nuestra estrategia Seeks para la consulta 4:
DECLARE
@numrows AS FLOAT = 1000000,
@numgroups AS FLOAT = 5,
@rowsperpage AS FLOAT = 404,
@groupsperpage AS FLOAT = 600;
SELECT
0.005666259259259 + CEILING(1e0 * @numgroups / @groupsperpage)
* 0.000740740740741 + @numgroups * 0.0000011
+ @numgroups * 0.00016229
+ (1e0 / (@numrows / @numgroups)) * (CEILING(1e0 * @numrows / @rowsperpage)
* (1e0 - POWER((CEILING(1e0 * @numrows / @rowsperpage) - 1e0)
/ CEILING(1e0 * @numrows / @rowsperpage), @numgroups - 1e0)) - 1e0)
* (0.003125 + (0.000740740740741 * (CEILING((@numrows / @rowsperpage)
* (1e0 / @numgroups)) - 1e0)))
AS seeksplancost; Este cálculo calcula el costo 0,0072295 para la Consulta 4. El costo estimado que se muestra en la Figura 3 es 0,0072299. ¡Eso está bastante cerca! Como ejercicio, calcule los costos para la Consulta 5 y la Consulta 6 usando esta fórmula y verifique que obtenga números cercanos a los que se muestran en la Figura 3.
Recuerde que la fórmula de cálculo de costos para la estrategia predeterminada basada en escaneo es (llámela Escaneo estrategia):
0.002549259259259 + CEILING(1e0 * @numrows / @rowsperpage) * 0.000740740740741 + @numrows * 0.0000017 + @numgroups * 0.0000005
Utilizando la consulta 1 como ejemplo y suponiendo 1 000 000 de filas en la tabla, 404 filas por página y 5 grupos, el costo estimado del plan de consultas de la estrategia de exploración es 3,5366.
La Figura 6 muestra los costos estimados del plan de consultas para las dos estrategias, aplicadas por Consulta 1 (escanear) y Consulta 4 (búsquedas), dado un número fijo de grupos de 5 y diferentes números de filas en la tabla principal.
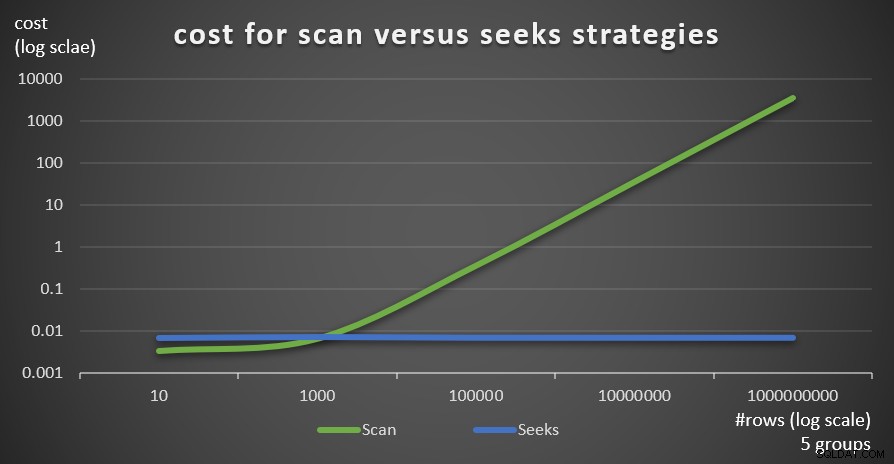Figura 6:costo de Escaneo versus estrategias de búsqueda (5 grupos)
La Figura 7 muestra los costos estimados del plan de consultas para las dos estrategias, dado un número fijo de filas en la tabla principal de 1 000 000 y diferentes números de grupos.
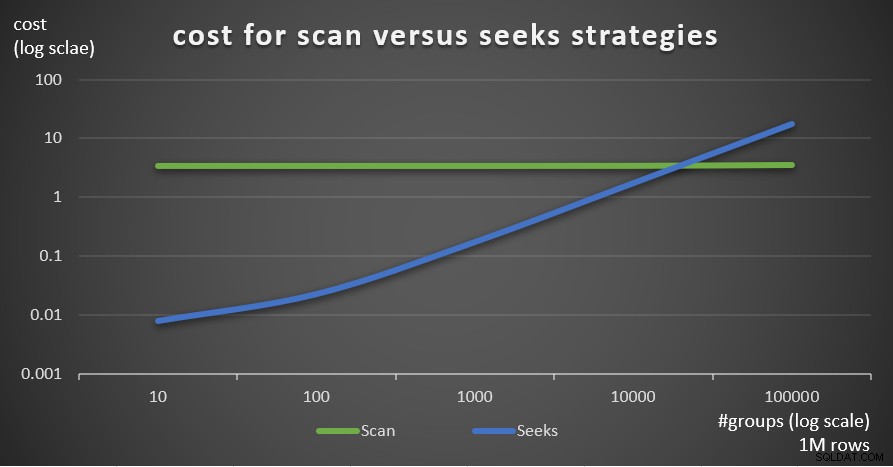Figura 7:costo de Escanear frente a estrategias de búsqueda (1 millón de filas)
Como es evidente a partir de estos hallazgos, cuanto mayor sea la densidad del conjunto de agrupación y más filas en la tabla principal, más óptima será la estrategia de búsqueda en comparación con la estrategia de exploración. Por lo tanto, en escenarios de alta densidad, asegúrese de probar la solución basada en APPLY. Mientras tanto, podemos esperar que Microsoft agregue esta estrategia como una opción integrada para consultas agrupadas.
Conclusión
Este artículo concluye una serie de cinco partes sobre los umbrales de optimización de consultas para consultas que agrupan y agregan datos. Uno de los objetivos de la serie era discutir los detalles de los diversos algoritmos que puede usar el optimizador, las condiciones bajo las cuales se prefiere cada algoritmo y cuándo debe intervenir con sus propias reescrituras de consultas. Otro objetivo era explicar el proceso de descubrir las distintas opciones y compararlas. Obviamente, el mismo proceso de análisis se puede aplicar al filtrado, unión, creación de ventanas y muchos otros aspectos de la optimización de consultas. Con suerte, ahora se siente más equipado que antes para lidiar con el ajuste de consultas.
