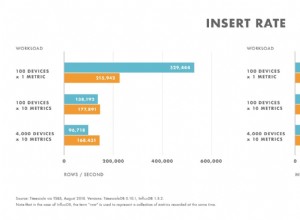
Una parte importante del ajuste de consultas es comprender los algoritmos que están disponibles para el optimizador para manejar varias construcciones de consultas, por ejemplo, filtrar, unir, agrupar y agregar, y cómo se escalan. Este conocimiento lo ayuda a preparar un entorno físico óptimo para sus consultas, como la creación de los índices correctos. También le ayuda a detectar de forma intuitiva qué algoritmo debe esperar ver en el plan en determinadas circunstancias, en función de su familiaridad con los umbrales en los que el optimizador debe cambiar de un algoritmo a otro. Luego, al ajustar las consultas de bajo rendimiento, puede detectar más fácilmente áreas en el plan de consulta donde el optimizador puede haber tomado decisiones subóptimas, por ejemplo, debido a estimaciones de cardinalidad inexactas, y tomar medidas para corregirlas.
Otra parte importante del ajuste de consultas es pensar fuera de la caja, más allá de los algoritmos que están disponibles para el optimizador cuando usa las herramientas obvias. Ser creativo. Supongamos que tiene una consulta que funciona mal a pesar de que organizó el entorno físico óptimo. Para las construcciones de consulta que usó, los algoritmos disponibles para el optimizador son x, y y z, y el optimizador eligió lo mejor que pudo según las circunstancias. Aún así, la consulta funciona mal. ¿Puedes imaginar un plan teórico con un algoritmo que pueda generar una consulta mucho mejor? Si puede imaginarlo, lo más probable es que pueda lograrlo con alguna reescritura de consulta, tal vez con construcciones de consulta menos obvias para la tarea.
En esta serie de artículos, me centro en agrupar y agregar datos. Comenzaré repasando los algoritmos que están disponibles para el optimizador cuando se usan consultas agrupadas. Luego describiré escenarios en los que ninguno de los algoritmos existentes funciona bien y mostraré reescrituras de consultas que dan como resultado un excelente rendimiento y escalabilidad.
Me gustaría agradecer a Craig Freedman, Vassilis Papadimos y Joe Sack, miembros de la intersección del conjunto de personas más inteligentes del planeta y el conjunto de desarrolladores de SQL Server, por responder a mis preguntas sobre la optimización de consultas.
Para los datos de muestra, usaré una base de datos llamada PerformanceV3. Puede descargar un script para crear y completar la base de datos desde aquí. Usaré una tabla llamada dbo.Orders, que se completa con 1 000 000 de filas. Esta tabla tiene un par de índices que no son necesarios y podrían interferir con mis ejemplos, así que ejecute el siguiente código para descartar esos índices innecesarios:
DROP INDEX idx_nc_sid_od_cid ON dbo.Orders; DROP INDEX idx_unc_od_oid_i_cid_eid ON dbo.Orders;
Los únicos dos índices que quedan en esta tabla son un índice agrupado llamado idx_cl_od en la columna orderdate y un índice único no agrupado llamado PK_Orders en la columna orderid, lo que impone la restricción de clave principal.
EXEC sys.sp_helpindex 'dbo.Orders';
index_name index_description index_keys ----------- ----------------------------------------------------- ----------- idx_cl_od clustered located on PRIMARY orderdate PK_Orders nonclustered, unique, primary key located on PRIMARY orderid
Algoritmos existentes
SQL Server admite dos algoritmos principales para agregar datos:Stream Aggregate y Hash Aggregate. Con consultas agrupadas, el algoritmo Stream Aggregate requiere que los datos estén ordenados por columnas agrupadas, por lo que debe distinguir entre dos casos. Uno es un Stream Aggregate preordenado, por ejemplo, cuando los datos se obtienen preordenados de un índice. Otro es un Stream Aggregate no preordenado, donde se requiere un paso adicional para ordenar explícitamente la entrada. Estos dos casos se escalan de manera muy diferente, por lo que también podría considerarlos como dos algoritmos diferentes.
El algoritmo Hash Aggregate organiza los grupos y sus agregados en una tabla hash. No requiere que se ordene la entrada.
Con suficientes datos, el optimizador considera paralelizar el trabajo, aplicando lo que se conoce como agregado local-global. En tal caso, la entrada se divide en varios subprocesos y cada subproceso aplica uno de los algoritmos antes mencionados para agregar localmente su subconjunto de filas. Luego, un agregado global usa uno de los algoritmos antes mencionados para agregar los resultados de los agregados locales.
En este artículo, me centro en el algoritmo Stream Aggregate pedido por adelantado y su escalado. En futuras partes de esta serie, cubriré otros algoritmos y describiré los umbrales en los que el optimizador cambia de uno a otro, y cuándo debe considerar la reescritura de consultas.
Agregado de flujo reservado
Dada una consulta agrupada con un conjunto de agrupación no vacío (el conjunto de expresiones por las que agrupa), el algoritmo Stream Aggregate requiere que las filas de entrada estén ordenadas por las expresiones que forman el conjunto de agrupación. Cuando el algoritmo procesa la primera fila de un grupo, inicializa un miembro que contiene el valor agregado intermedio con el valor relevante (por ejemplo, el valor de la primera fila para un agregado MAX). Cuando procesa una fila que no es la primera en el grupo, asigna a ese miembro el resultado de un cálculo que involucra el valor agregado intermedio y el valor de la nueva fila (por ejemplo, el máximo entre el valor agregado intermedio y el valor nuevo). Tan pronto como cualquiera de los miembros del conjunto de agrupación cambia su valor, o se consume la entrada, el valor agregado actual se considera el resultado final para el último grupo.
Una forma de ordenar los datos como necesita el algoritmo Stream Aggregate es obtenerlos ordenados previamente a partir de un índice. Necesita que el índice se defina con las columnas del conjunto de agrupación como claves, en cualquier orden entre ellas. También desea que el índice cubra. Por ejemplo, considere la siguiente consulta (la llamaremos Consulta 1):
SELECT shipperid, MAX(orderdate) AS maxorderid FROM dbo.Orders GROUP BY shipperid;
Un índice de almacén de filas óptimo para admitir esta consulta sería uno definido con shipperid como la columna de clave principal y orderdate como una columna incluida o como una segunda columna de clave:
CREATE INDEX idx_sid_od ON dbo.Orders(shipperid, orderdate);
Con este índice en su lugar, obtiene el plan estimado que se muestra en la Figura 1 (usando SentryOne Plan Explorer).

Figura 1:Plan para Consulta 1
Tenga en cuenta que el operador Index Scan tiene una propiedad Ordered:True que significa que es necesario entregar las filas ordenadas por la clave de índice. El operador Stream Aggregate luego ingiere las filas ordenadas como las necesita. En cuanto a cómo se calcula el costo del operador; antes de llegar a eso, un prefacio rápido primero...
Como ya sabrá, cuando SQL Server optimiza una consulta, evalúa múltiples planes candidatos y finalmente elige el que tiene el costo estimado más bajo. El costo estimado del plan es la suma de todos los costos estimados de los operadores. A su vez, el costo estimado de cada operador es la suma del costo de E/S estimado y el costo de CPU estimado. La unidad de costo no tiene sentido por derecho propio. Su relevancia está en la comparación que hace el optimizador entre planes candidatos. Es decir, las fórmulas de cálculo de costos se diseñaron con el objetivo de que, entre los planes candidatos, el que tenga el costo más bajo represente (con suerte) el que terminará más rápido. ¡Una tarea terriblemente compleja de hacer con precisión!
Cuanto más tengan en cuenta las fórmulas de costeo los factores que realmente afectan el rendimiento y la escala del algoritmo, más precisas serán y más probable será que, dadas las estimaciones de cardinalidad precisas, el optimizador elija el plan óptimo. En cualquier caso, si desea comprender por qué el optimizador elige un algoritmo en lugar de otro, debe comprender dos cosas principales:una es cómo funcionan y se escalan los algoritmos, y otra es el modelo de costos de SQL Server.
Volvamos al plan de la Figura 1; tratemos de entender cómo se calculan los costos. Como política, Microsoft no revelará las fórmulas de cálculo de costos internos que utilizan. Cuando era niño me fascinaba desarmar cosas. Relojes, radios, cintas de cassette (sí, soy tan viejo), lo que sea. Quería saber cómo se hacían las cosas. Del mismo modo, veo valor en la ingeniería inversa de las fórmulas, ya que si logro predecir el costo con una precisión razonable, probablemente signifique que entiendo bien el algoritmo. Durante el proceso aprendes mucho.
Nuestra consulta ingiere 1,000,000 de filas. Incluso con esta cantidad de filas, el costo de E/S parece ser insignificante en comparación con el costo de la CPU, por lo que probablemente sea seguro ignorarlo.
En cuanto al costo de la CPU, desea intentar averiguar qué factores lo afectan y de qué manera. En teoría, podría haber una serie de factores:número de filas de entrada, número de grupos, cardinalidad del conjunto de agrupación, tipo de datos y tamaño de los miembros del conjunto de agrupación. Entonces, para probar y medir el efecto de cualquiera de estos factores, desea comparar los costos estimados de dos consultas que difieren solo en el factor que desea medir. Por ejemplo, para medir el impacto del número de filas en el costo, tenga dos consultas con un número diferente de filas de entrada, pero con todos los demás aspectos iguales (número de grupos, cardinalidad del conjunto de agrupación, etc.). Además, es importante verificar que los números estimados, no los reales, sean los deseados, ya que el optimizador se basa en los números estimados para calcular los costos.
Al hacer tales comparaciones, es bueno tener técnicas que le permitan controlar completamente los números estimados. Por ejemplo, una forma sencilla de controlar el número estimado de filas de entrada es consultar una expresión de tabla que se basa en una consulta TOP y aplicar la función agregada en la consulta externa. Si le preocupa que, debido a su uso del operador SUPERIOR, el optimizador aplique objetivos de fila y que estos resulten en un ajuste de los costos originales, esto solo se aplica a los operadores que aparecen en el plan debajo del operador Superior (al derecha), no arriba (a la izquierda). El operador Stream Aggregate aparece de forma natural sobre el operador Top en el plan, ya que ingiere las filas filtradas.
En cuanto al control del número estimado de grupos de salida, puede hacerlo mediante la expresión de agrupación
Para asegurarse de obtener el algoritmo Stream Aggregate y un plan en serie, puede forzar esto con las sugerencias de consulta:OPCIÓN (GRUPO DE ORDEN, MAXDOP 1).
También desea averiguar si hay algún costo inicial para el operador para que pueda tenerlo en cuenta en su fórmula de ingeniería inversa.
Comencemos por averiguar la forma en que la cantidad de filas de entrada afecta el costo de CPU estimado del operador. Claramente, este factor debería ser relevante para el costo del operador. Además, esperaría que el costo por fila fuera constante. Aquí hay un par de consultas para comparar que difieren solo en el número estimado de filas de entrada (llámelas Consulta 2 y Consulta 3, respectivamente):
SELECT orderid % 10000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (100000) * FROM dbo.Orders) AS D GROUP BY orderid % 10000 OPTION(ORDER GROUP, MAXDOP 1); SELECT orderid % 10000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (200000) * FROM dbo.Orders) AS D GROUP BY orderid % 10000 OPTION(ORDER GROUP, MAXDOP 1);
La Figura 2 tiene las partes relevantes de los planes estimados para estas consultas:

Figura 2:Planes para Consulta 2 y Consulta 3
Suponiendo que el costo por fila es constante, puede calcularlo como la diferencia entre los costos del operador dividida por la diferencia entre las cardinalidades de entrada del operador:
CPU cost per row = (0.125 - 0.065) / (200000 - 100000) = 0.0000006
Para verificar que el número que obtuvo es realmente constante y correcto, puede intentar predecir los costos estimados en consultas con otros números de filas de entrada. Por ejemplo, el costo previsto con 500 000 filas de entrada es:
Cost for 500K input rows = <cost for 100K input rows> + 400000 * 0.0000006 = 0.065 + 0.24 = 0.305
Utilice la siguiente consulta para verificar si su predicción es precisa (llámela Consulta 4):
SELECT orderid % 10000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (500000) * FROM dbo.Orders) AS D GROUP BY orderid % 10000 OPTION(ORDER GROUP, MAXDOP 1);
La parte relevante del plan para esta consulta se muestra en la Figura 3.
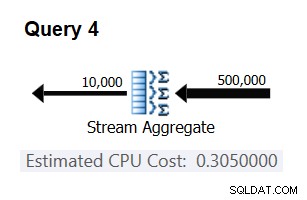
Figura 3:Plan para Consulta 4
Bingo. Naturalmente, es una buena idea verificar múltiples cardinalidades de entrada adicionales. Con todos los que revisé, la tesis de que hay un costo constante por fila de entrada de 0.0000006 era correcta.
A continuación, intentemos averiguar cómo el número estimado de grupos afecta el costo de la CPU del operador. Es de esperar que se necesite algo de trabajo de CPU para procesar cada grupo, y también es razonable esperar que sea constante por grupo. Para probar esta tesis y calcular el costo por grupo, puede usar las siguientes dos consultas, que difieren solo en la cantidad de grupos de resultados (llámelas Consulta 5 y Consulta 6, respectivamente):
SELECT orderid % 10000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (100000) * FROM dbo.Orders) AS D GROUP BY orderid % 10000 OPTION(ORDER GROUP, MAXDOP 1); SELECT orderid % 20000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (100000) * FROM dbo.Orders) AS D GROUP BY orderid % 20000 OPTION(ORDER GROUP, MAXDOP 1);
Las partes relevantes de los planes de consulta estimados se muestran en la Figura 4.
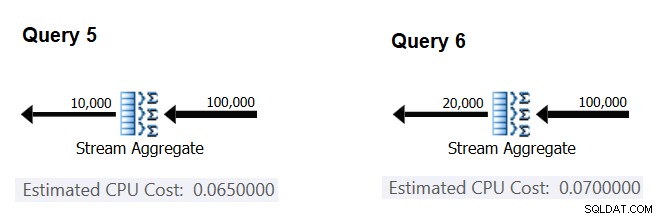
Figura 4:Planes para Consulta 5 y Consulta 6
De forma similar a como calculó el costo fijo por fila de entrada, puede calcular el costo fijo por grupo de salida como la diferencia entre los costos del operador dividida por la diferencia entre las cardinalidades de salida del operador:
CPU cost per group = (0.07 - 0.065) / (20000 - 10000) = 0.0000005
Y tal como lo demostré antes, puede verificar sus hallazgos prediciendo los costos con otros números de grupos de salida y comparando sus números pronosticados con los producidos por el optimizador. Con todos los grupos que probé, los costos pronosticados fueron precisos.
Usando técnicas similares, puede verificar si otros factores afectan el costo del operador. Mis pruebas muestran que la cardinalidad del conjunto de agrupación (número de expresiones por las que agrupa), los tipos de datos y los tamaños de las expresiones agrupadas no tienen impacto en el costo estimado.
Lo que queda es verificar si se asume algún costo inicial significativo para el operador. Si hay una, la fórmula completa (con suerte) para calcular el costo de la CPU del operador debería ser:
Operator CPU cost = <startup cost> + <#input rows> * 0.0000006 + <#output groups> * 0.0000005
Para que pueda derivar el costo inicial del resto:
Startup cost =- (<#input rows> * 0.0000006 + <#output groups> * 0.0000005)
Puede usar cualquier plan de consulta de este artículo para este propósito. Por ejemplo, al usar los números del plan para la Consulta 5 que se muestra anteriormente en la Figura 4, obtiene:
Startup cost = 0.065 - (100000 * 0.0000006 + 10000 * 0.0000005) = 0
Como parece, el operador Stream Aggregate no tiene ningún costo de inicio relacionado con la CPU, o es tan bajo que no se muestra con la precisión de la medida de costo.
En conclusión, la fórmula de ingeniería inversa para el costo del operador de Stream Aggregate es:
I/O cost: negligible CPU cost: <#input rows> * 0.0000006 + <#output groups> * 0.0000005
La Figura 5 muestra la escala del costo del operador Stream Aggregate con respecto a la cantidad de filas y la cantidad de grupos.
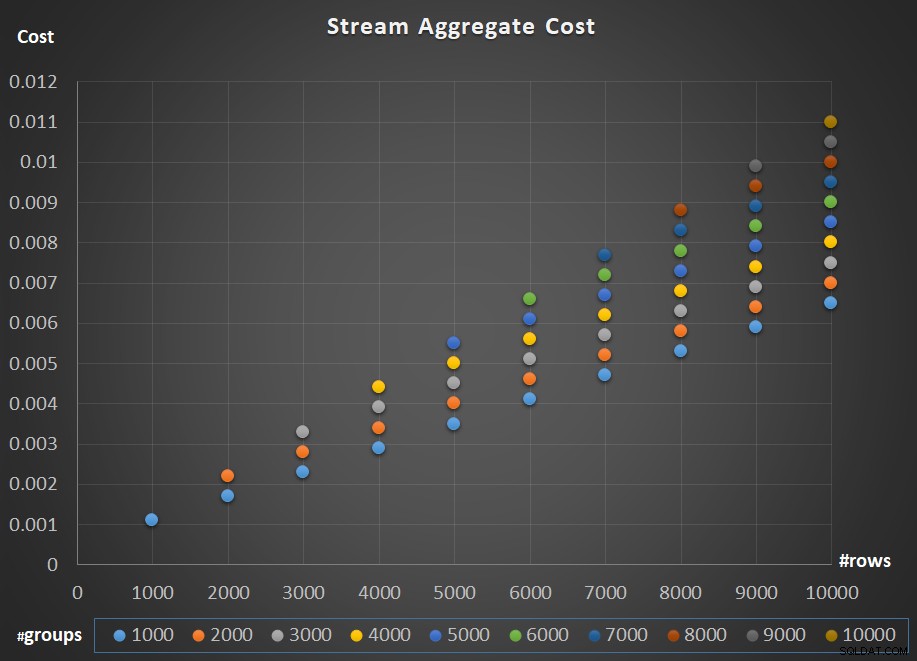
Figura 5:Gráfico de escalado del algoritmo Stream Aggregate
En cuanto al escalado del operador; es lineal. En los casos en que el número de grupos tiende a ser proporcional al número de filas, el costo total del operador aumenta por el mismo factor que aumenta tanto el número de filas como el de grupos. Lo que significa que duplicar el número de filas de entrada y grupos de entrada da como resultado la duplicación del costo total del operador. Para ver por qué, supongamos que representamos el costo del operador como:
r * 0.0000006 + g * 0.0000005
Si aumenta tanto el número de filas como el número de grupos por el mismo factor p, obtiene:
pr * 0.0000006 + pg * 0.0000005 = p * (r * 0.0000006 + g * 0.0000005)
Entonces, si, para un número determinado de filas y grupos, el costo del operador Stream Aggregate es C, aumentar tanto el número de filas como de grupos por el mismo factor p da como resultado un costo de operador de pC. Vea si puede verificar esto identificando ejemplos en el cuadro de la Figura 5.
En los casos en que la cantidad de grupos se mantiene bastante estable incluso cuando la cantidad de filas de entrada crece, aún obtiene una escala lineal. Simplemente considere el costo asociado con el número de grupos como una constante. Es decir, si para un número dado de filas y grupos el costo del operador es C =G (costo asociado con el número de grupos) más R (costo asociado con el número de filas), aumentando solo el número de filas por un factor de p da como resultado G + pR. En tal caso, naturalmente, el costo total del operador es menor que pC. Es decir, duplicar el número de filas da como resultado menos del doble del costo total del operador.
En la práctica, en muchos casos, cuando agrupa datos, la cantidad de filas de entrada es sustancialmente mayor que la cantidad de grupos de salida. Este hecho, combinado con el hecho de que el costo asignado por fila y el costo por grupo son casi iguales, la porción del costo del operador que se atribuye al número de grupos se vuelve insignificante. Como ejemplo, vea el plan para la Consulta 1 que se muestra anteriormente en la Figura 1. En tales casos, es seguro pensar en el costo del operador simplemente escalando linealmente con respecto al número de filas de entrada.
Casos especiales
Hay casos especiales en los que el operador Stream Aggregate no necesita ordenar los datos en absoluto. Si lo piensa, el algoritmo Stream Aggregate tiene un requisito de ordenación más relajado desde la entrada en comparación con cuando necesita los datos ordenados para fines de presentación, por ejemplo, cuando la consulta tiene una cláusula ORDER BY de presentación externa. El algoritmo Stream Aggregate simplemente necesita que todas las filas del mismo grupo se ordenen juntas. Tome el conjunto de entrada {5, 1, 5, 2, 1, 2}. Para fines de ordenación de presentaciones, este conjunto debe ordenarse así:1, 1, 2, 2, 5, 5. Para fines de agregación, el algoritmo Stream Aggregate aún funcionaría bien si los datos se organizaran en el siguiente orden:5, 5, 1, 1, 2, 2. Con esto en mente, cuando calcula un agregado escalar (consulta con una función agregada y sin cláusula GROUP BY) o agrupa los datos por un conjunto de agrupación vacío, nunca hay más de un grupo . Independientemente del orden de las filas de entrada, se puede aplicar el algoritmo Stream Aggregate. El algoritmo Hash Aggregate procesa los datos en función de las expresiones del conjunto de agrupación como entradas, y tanto con agregados escalares como con un conjunto de agrupación vacío, no hay entradas para realizar el hash. Por lo tanto, tanto con agregados escalares como con agregados aplicados a un conjunto de agrupación vacío, el optimizador siempre usa el algoritmo Stream Aggregate, sin necesidad de ordenar previamente los datos. Ese es al menos el caso en el modo de ejecución de filas, ya que actualmente (a partir de SQL Server 2017 CU4) el modo por lotes solo está disponible con el algoritmo Hash Aggregate. Usaré las siguientes dos consultas para demostrar esto (llámelas Consulta 7 y Consulta 8):
SELECT COUNT(*) AS numrows FROM dbo.Orders; SELECT COUNT(*) AS numrows FROM dbo.Orders GROUP BY ();
Los planes para estas consultas se muestran en la Figura 6.
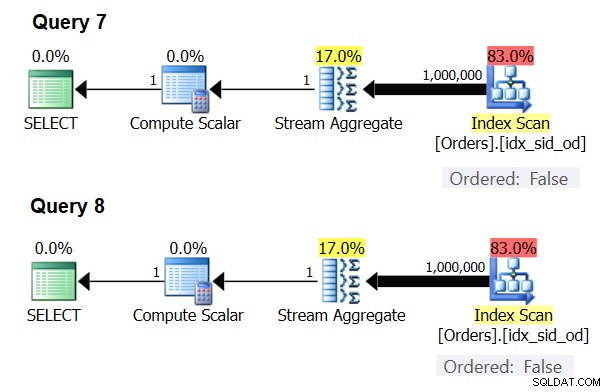
Figura 6:Planes para Consulta 7 y Consulta 8
Intente forzar un algoritmo Hash Aggregate en ambos casos:
SELECT COUNT(*) AS numrows FROM dbo.Orders OPTION(HASH GROUP); SELECT COUNT(*) AS numrows FROM dbo.Orders GROUP BY () OPTION(HASH GROUP);
El optimizador ignora su solicitud y produce los mismos planes que se muestran en la Figura 6.
Prueba rápida:¿cuál es la diferencia entre un agregado escalar y un agregado aplicado a un conjunto de agrupación vacío?
Respuesta:con un conjunto de entrada vacío, un agregado escalar devuelve un resultado con una fila, mientras que un agregado en una consulta con un conjunto de agrupación vacío devuelve un conjunto de resultados vacío. Pruébalo:
SELECT COUNT(*) AS numrows FROM dbo.Orders WHERE 1 = 2;
numrows ----------- 0 (1 row affected)
SELECT COUNT(*) AS numrows FROM dbo.Orders WHERE 1 = 2 GROUP BY ();
numrows ----------- (0 rows affected)
Cuando haya terminado, ejecute el siguiente código para la limpieza:
DROP INDEX idx_sid_od ON dbo.Orders;
Resumen y desafío
La ingeniería inversa de la fórmula de costos para el algoritmo Stream Aggregate es un juego de niños. Podría haberle dicho que la fórmula de costos para un algoritmo Stream Aggregate pedido por adelantado es @numrows * 0.0000006 + @numgroups * 0.0000005 en lugar de un artículo completo para explicar cómo resolver esto. Sin embargo, el objetivo era describir el proceso y los principios de la ingeniería inversa, antes de pasar a los algoritmos más complejos y los umbrales en los que un algoritmo se vuelve más óptimo que los demás. Enseñarte a pescar en lugar de darte pescado. Aprendí mucho y descubrí cosas en las que ni siquiera había pensado, mientras intentaba aplicar ingeniería inversa a fórmulas de costos para varios algoritmos.
¿Listo para poner a prueba tus habilidades? Su misión, si decide aceptarla, es un poco más difícil que la ingeniería inversa del operador Stream Aggregate. Aplicar ingeniería inversa a la fórmula de costeo de un operador Ordenar en serie. Esto es importante para nuestra investigación ya que un algoritmo Stream Aggregate aplicado para una consulta con un conjunto de agrupación no vacío, donde los datos de entrada no están ordenados previamente, requiere una clasificación explícita. En tal caso, el costo y la escala de la operación agregada dependen del costo y la escala de los operadores Sort y Stream Aggregate combinados.
Si logra acercarse decentemente a la predicción del costo del operador Ordenar, puede sentir que se ganó el derecho de agregar a su firma "Ingeniería inversa". Hay muchos ingenieros de software por ahí; ¡pero ciertamente no ves muchos ingenieros inversos! Solo asegúrese de probar su fórmula tanto con números pequeños como con números grandes; puede que te sorprenda lo que encuentres.