Igualar la oferta con la demanda:soluciones, parte 2

[ Saltar a:Desafío original | Soluciones:Parte 1 | Parte 2 | Parte 3 ]

En este artículo, continúo con la cobertura de las soluciones al tentador desafío de emparejar la oferta con la demanda de Peter Larsson. Gracias de nuevo a Luca, Kamil Kosno, Daniel Brown, Brian Walker, Joe Obbish, Rainer Hoffmann, Paul White, Charlie y Peter Larsson por enviarnos sus soluciones.

El mes pasado cubrí una solución basada en intersecciones de intervalos, utilizando una prueba clásica de intersección de intervalos basada en predicados. Me referiré a esa solución como intersecciones clásicas . El enfoque clásico de intersecciones de intervalos da como resultado un plan con escala cuadrática (N^2). Demostré su bajo rendimiento frente a entradas de muestra que van desde 100 000 a 400 000 filas. ¡La solución tardó 931 segundos en completarse contra la entrada de 400 000 filas! Este mes comenzaré recordándole brevemente la solución del mes pasado y por qué escala y funciona tan mal. Luego presentaré un enfoque basado en una revisión de la prueba de intersección de intervalos. Este enfoque fue utilizado por Luca, Kamil y posiblemente también por Daniel, y permite una solución con mucho mejor rendimiento y escalabilidad. Me referiré a esa solución como intersecciones revisadas .

El problema con la prueba de intersección clásica

Comencemos con un recordatorio rápido de la solución del mes pasado.

Usé los siguientes índices en la tabla de entrada dbo.Auctions para respaldar el cálculo de los totales acumulados que producen los intervalos de oferta y demanda:

-- Index to support solution
 
CREATE UNIQUE NONCLUSTERED INDEX idx_Code_ID_i_Quantity
  ON dbo.Auctions(Code, ID)
  INCLUDE(Quantity);
 
-- Enable batch-mode Window Aggregate
 
CREATE NONCLUSTERED COLUMNSTORE INDEX idx_cs
  ON dbo.Auctions(ID)
  WHERE ID = -1 AND ID = -2;

El siguiente código tiene la solución completa que implementa el enfoque clásico de intersecciones de intervalos:

-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID,
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID, 
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_ES_ID ON #Supply(EndSupply, ID);
 
-- Trades are the overlapping segments of the intersecting intervals
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S WITH (FORCESEEK)
    ON D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply;

Este código comienza calculando los intervalos de oferta y demanda y escribiéndolos en tablas temporales llamadas #Demand y #Supply. Luego, el código crea un índice agrupado en #Supply con EndSupply como la clave principal para respaldar la prueba de intersección de la mejor manera posible. Finalmente, el código une #Oferta y #Demanda, identificando transacciones como los segmentos superpuestos de los intervalos que se cruzan, utilizando el siguiente predicado de unión basado en la prueba clásica de intersección de intervalos:

D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply

El plan para esta solución se muestra en la Figura 1.

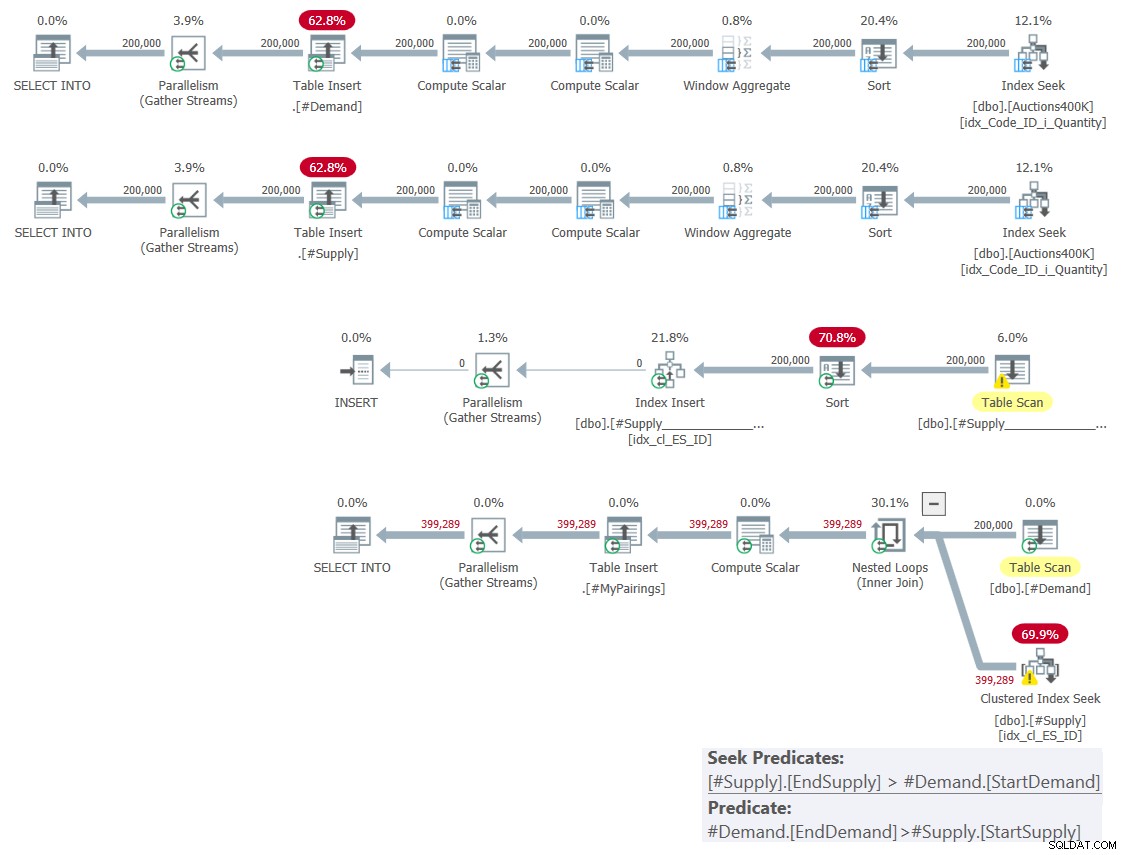Figura 1:Plan de consulta para solución basada en intersecciones clásicas

Como expliqué el mes pasado, entre los dos predicados de rango involucrados, solo uno puede usarse como predicado de búsqueda como parte de una operación de búsqueda de índice, mientras que el otro debe aplicarse como predicado residual. Puede ver esto claramente en el plan de la última consulta en la Figura 1. Es por eso que solo me molesté en crear un índice en una de las tablas. También forcé el uso de una búsqueda en el índice que creé usando la sugerencia FORCESEEK. De lo contrario, el optimizador podría terminar ignorando ese índice y creando uno propio usando un operador Index Spool.

Este plan tiene complejidad cuadrática ya que por fila en un lado, #Demanda en nuestro caso, la búsqueda de índice tendrá que acceder en promedio a la mitad de las filas en el otro lado, #Oferta en nuestro caso, en función del predicado de búsqueda e identificar el coincidencias finales aplicando el predicado residual.

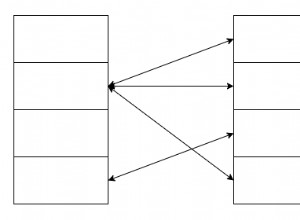
Si aún no le queda claro por qué este plan tiene una complejidad cuadrática, tal vez una representación visual del trabajo podría ayudar, como se muestra en la Figura 2.

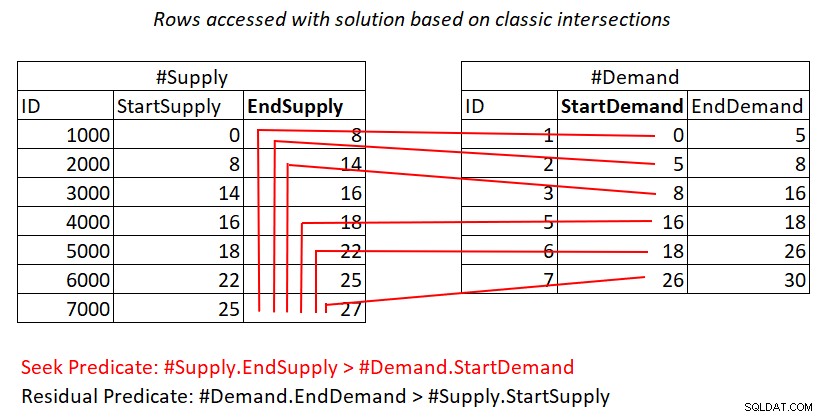Figura 2:Ilustración de trabajo con solución basada en intersecciones clásicas

Esta ilustración representa el trabajo realizado por la combinación de bucles anidados en el plan para la última consulta. El montón #Demand es la entrada externa de la combinación y el índice agrupado en #Supply (con EndSupply como clave principal) es la entrada interna. Las líneas rojas representan las actividades de búsqueda de índice realizadas por fila en #Demand en el índice de #Supply y las filas a las que acceden como parte de los escaneos de rango en la hoja de índice. Hacia valores extremadamente bajos de StartDemand en #Demand, el escaneo de rango necesita acceder cerca de todas las filas en #Supply. Hacia valores extremadamente altos de StartDemand en #Demand, el escaneo de rango necesita acceder a filas cercanas a cero en #Supply. En promedio, el escaneo de rango necesita acceder a aproximadamente la mitad de las filas en #Supply por fila en demanda. Con filas de demanda D y filas de oferta S, el número de filas a las que se accede es D + D*S/2. Eso se suma al costo de las búsquedas que lo llevan a las filas correspondientes. Por ejemplo, al llenar dbo.Auctions con 200 000 filas de demanda y 200 000 filas de oferta, esto se traduce en la combinación de bucles anidados que accede a 200 000 filas de demanda + 200 000*200 000/2 filas de oferta, o 200 000 + 200 000^2/2 =20 000 200 000 filas accedidas. ¡Aquí se están volviendo a escanear muchas filas de suministros!

Si desea ceñirse a la idea de las intersecciones de intervalos pero obtener un buen rendimiento, debe idear una manera de reducir la cantidad de trabajo realizado.

En su solución, Joe Obbish dividió en cubos los intervalos en función de la duración máxima del intervalo. De esta forma, pudo reducir la cantidad de filas que las uniones necesitaban manejar y confiar en el procesamiento por lotes. Usó la prueba clásica de intersección de intervalos como filtro final. La solución de Joe funciona bien siempre que la duración máxima del intervalo no sea muy alta, pero el tiempo de ejecución de la solución aumenta a medida que aumenta la duración máxima del intervalo.

Entonces, ¿qué más puedes hacer...?

Prueba de intersección revisada

Luca, Kamil y posiblemente Daniel (había una parte poco clara sobre su solución publicada debido al formato del sitio web, así que tuve que adivinar) usaron una prueba de intersección de intervalo revisada que permite una mejor utilización de la indexación.

Su prueba de intersección es una disyunción de dos predicados (predicados separados por el operador OR):

   (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply >= D.StartDemand AND S.StartSupply < D.EndDemand)

En inglés, el delimitador de inicio de demanda se cruza con el intervalo de suministro de manera inclusiva y exclusiva (incluido el inicio y excluyendo el final); o el delimitador de inicio de suministro se cruza con el intervalo de demanda, de manera inclusiva, exclusiva. Para hacer que los dos predicados sean disjuntos (que no tengan casos superpuestos) y aún así completos para cubrir todos los casos, puede mantener el operador =en solo uno u otro, por ejemplo:

   (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand)

Esta prueba de intersección de intervalos revisada es bastante reveladora. Cada uno de los predicados puede potencialmente usar eficientemente un índice. Considere el predicado 1:

D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
^^^^^^^^^^^^^                      ^^^^^^^^^^^^^

Suponiendo que crea un índice de cobertura en #Demand con StartDemand como clave principal, puede obtener una combinación de bucles anidados aplicando el trabajo ilustrado en la figura 3.

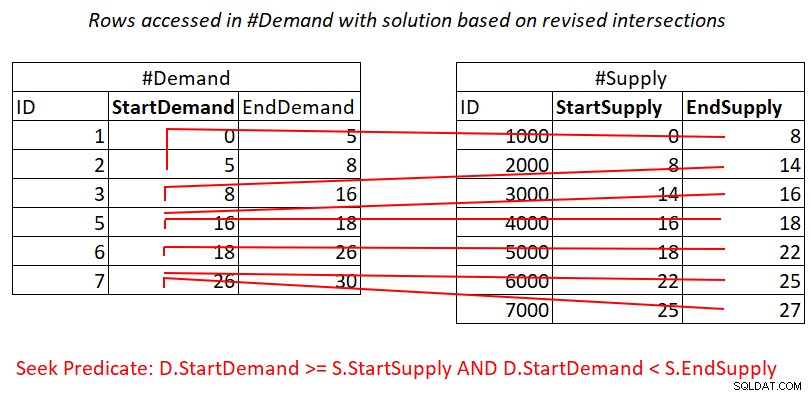
Figura 3:Ilustración del trabajo teórico requerido para procesar el predicado 1

Sí, aún paga por una búsqueda en el índice de #Demanda por fila en #Suministro, pero los escaneos de rango en la hoja de índice acceden a subconjuntos de filas casi inconexos. ¡Sin volver a escanear las filas!

La situación es similar con el predicado 2:

S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand
^^^^^^^^^^^^^                     ^^^^^^^^^^^^^

Suponiendo que crea un índice de cobertura en #Supply con StartSupply como clave principal, puede obtener una combinación de bucles anidados aplicando el trabajo ilustrado en la figura 4.

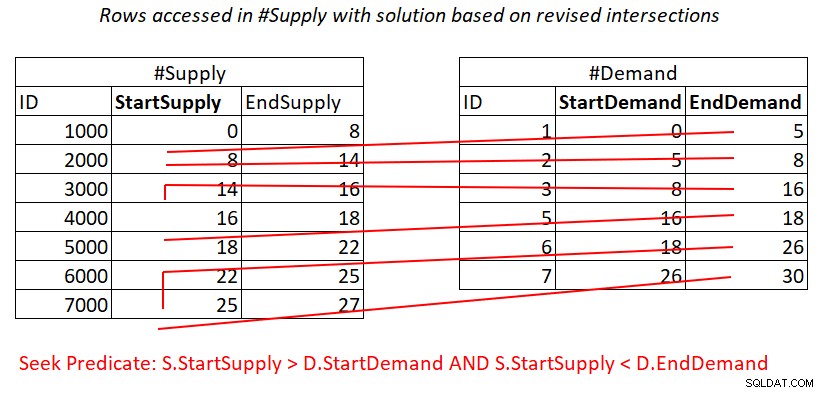
Figura 4:Ilustración del trabajo teórico requerido para procesar el predicado 2

Además, aquí paga por una búsqueda en el índice #Supply por fila en #Demand, y luego los escaneos de rango en la hoja de índice acceden a subconjuntos de filas casi separados. De nuevo, ¡no hay que volver a escanear las filas!

Suponiendo filas de demanda D y filas de oferta S, el trabajo se puede describir como:

Number of index seek operations: D  + S
Number of rows accessed:         2D + 2S

Es muy probable que la mayor parte del costo aquí sea el costo de E/S relacionado con las búsquedas. Pero esta parte del trabajo tiene una escala lineal en comparación con la escala cuadrática de la consulta clásica de intersecciones de intervalos.

Por supuesto, debe considerar el costo preliminar de la creación del índice en las tablas temporales, que tiene una escala n log n debido a la clasificación involucrada, pero paga esta parte como una parte preliminar de ambas soluciones.

Intentemos llevar esta teoría a la práctica. Comencemos llenando las tablas temporales #Demand y #supply con los intervalos de oferta y demanda (igual que con las intersecciones de intervalos clásicas) y creando los índices de soporte:

-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID, 
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID, 
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply,   0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
-- Indexing
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID);

Los planes para llenar las tablas temporales y crear los índices se muestran en la Figura 5.

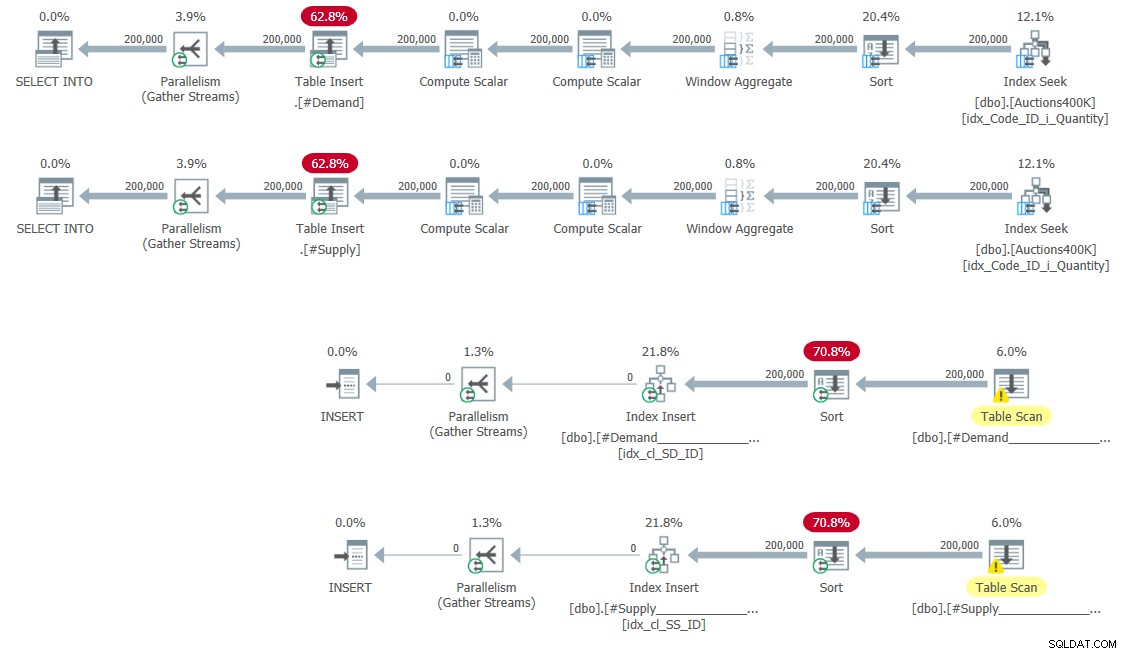
Figura 5:planes de consulta para completar tablas temporales y crear índices

Aquí no hay sorpresas.

Ahora a la consulta final. Es posible que tenga la tentación de utilizar una sola consulta con la disyunción de dos predicados antes mencionada, así:

SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply >  D.StartDemand AND S.StartSupply < D.EndDemand);

El plan para esta consulta se muestra en la Figura 6.

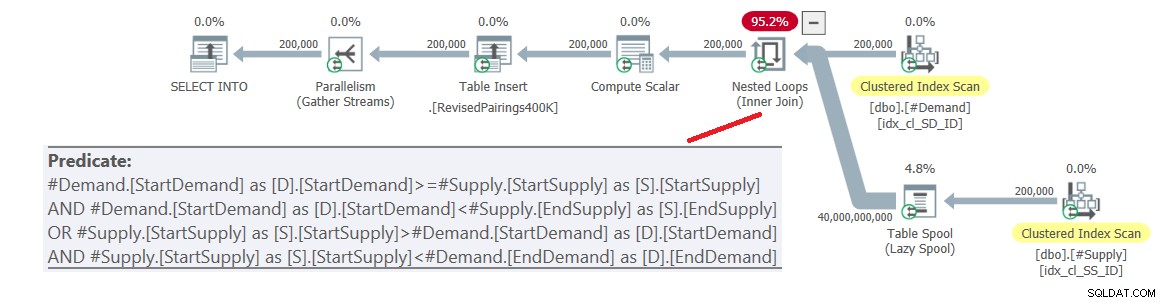
Figura 6:Plan de consulta para consulta final usando intersección revisada prueba, prueba 1

El problema es que el optimizador no sabe cómo dividir esta lógica en dos actividades separadas, cada una de las cuales maneja un predicado diferente y utiliza el índice respectivo de manera eficiente. Entonces, termina con un producto cartesiano completo de los dos lados, aplicando todos los predicados como predicados residuales. Con 200 000 filas de demanda y 200 000 filas de oferta, la unión procesa 40 000 000 000 filas.

El ingenioso truco utilizado por Luca, Kamil y posiblemente Daniel fue dividir la lógica en dos consultas, unificando sus resultados. ¡Ahí es donde el uso de dos predicados disjuntos se vuelve importante! Puede usar un operador UNION ALL en lugar de UNION, evitando el costo innecesario de buscar duplicados. Aquí está la consulta que implementa este enfoque:

SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
 
UNION ALL
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand;

El plan para esta consulta se muestra en la Figura 7.

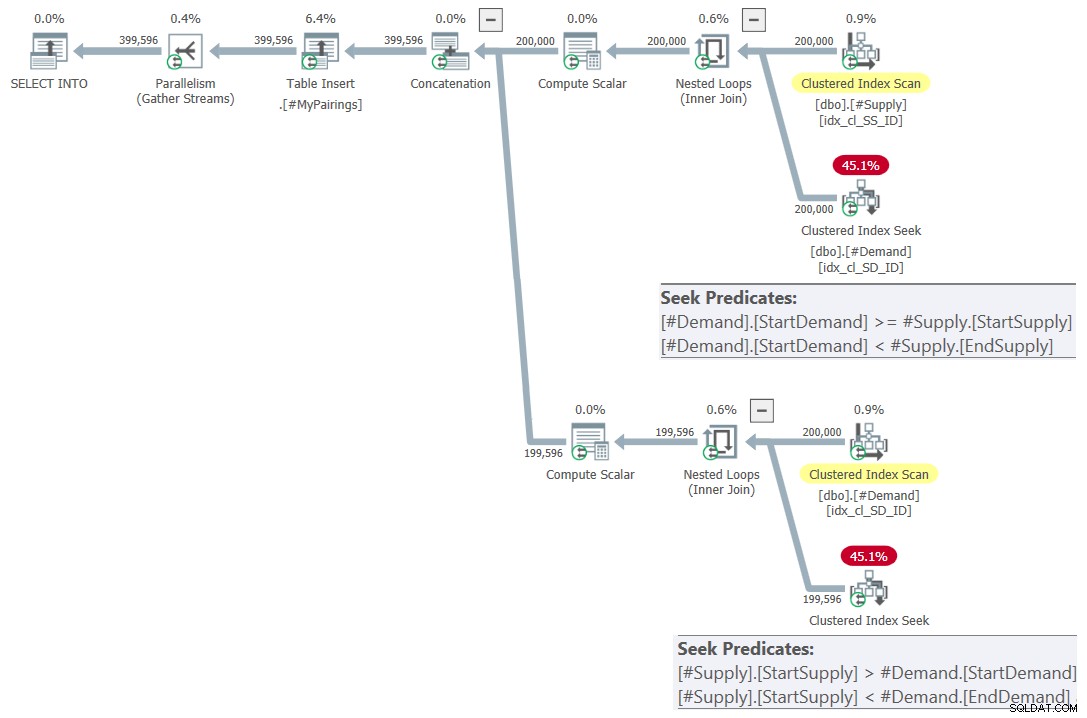
Figura 7:Plan de consulta para consulta final usando intersección revisada prueba, prueba 2

¡Esto es simplemente hermoso! ¿no es así? Y debido a que es tan hermoso, aquí está la solución completa desde cero, incluida la creación de tablas temporales, la indexación y la consulta final:

-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID, 
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID,
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply,   0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
-- Indexing
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID);
 
-- Trades are the overlapping segments of the intersecting intervals
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
 
UNION ALL
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand;

Como se mencionó anteriormente, me referiré a esta solución como intersecciones revisadas .

La solución de Kamil

Entre las soluciones de Luca, Kamil y Daniel, la de Kamil fue la más rápida. Aquí está la solución completa de Kamil:

SET NOCOUNT ON;
DROP TABLE IF EXISTS #supply, #demand;
GO
 
CREATE TABLE #demand
(
  DemandID           INT NOT NULL,
  DemandQuantity     DECIMAL(19, 6) NOT NULL,
  QuantityFromDemand DECIMAL(19, 6) NOT NULL,
  QuantityToDemand   DECIMAL(19, 6) NOT NULL
);
 
CREATE TABLE #supply
(
  SupplyID           INT NOT NULL,
  QuantityFromSupply DECIMAL(19, 6) NOT NULL,
  QuantityToSupply   DECIMAL(19,6) NOT NULL
);
 
WITH demand AS
(
  SELECT
    a.ID AS DemandID,
    a.Quantity AS DemandQuantity,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      - a.Quantity AS QuantityFromDemand,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      AS QuantityToDemand
  FROM dbo.Auctions AS a WHERE Code = 'D'
)
INSERT INTO #demand
(
  DemandID,
  DemandQuantity,
  QuantityFromDemand,
  QuantityToDemand
)
SELECT
  d.DemandID,
  d.DemandQuantity,
  d.QuantityFromDemand,
  d.QuantityToDemand
FROM demand AS d;
 
WITH supply AS
(
  SELECT
    a.ID AS SupplyID,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      - a.Quantity AS QuantityFromSupply,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      AS QuantityToSupply
  FROM dbo.Auctions AS a WHERE Code = 'S'
)
INSERT INTO #supply
(
  SupplyID,
  QuantityFromSupply,
  QuantityToSupply
)
SELECT
  s.SupplyID,
  s.QuantityFromSupply,
  s.QuantityToSupply
FROM supply AS s;
 
CREATE UNIQUE INDEX ix_1 ON #demand(QuantityFromDemand) 
  INCLUDE(DemandID, DemandQuantity, QuantityToDemand);
CREATE UNIQUE INDEX ix_1 ON #supply(QuantityFromSupply) 
  INCLUDE(SupplyID, QuantityToSupply);
CREATE NONCLUSTERED COLUMNSTORE INDEX nci ON #demand(DemandID) 
  WHERE DemandID is null;
 
DROP TABLE IF EXISTS #myPairings;
 
CREATE TABLE #myPairings
(
  DemandID      INT NOT NULL,
  SupplyID      INT NOT NULL,
  TradeQuantity DECIMAL(19, 6) NOT NULL
);
 
INSERT INTO #myPairings(DemandID, SupplyID, TradeQuantity) 
  SELECT
    d.DemandID,
    s.SupplyID, 
    d.DemandQuantity
      - CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply 
             THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 end
      - CASE WHEN s.QuantityToSupply < d.QuantityToDemand 
             THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity 
  FROM #demand AS d 
    INNER JOIN #supply AS s 
      ON (d.QuantityFromDemand < s.QuantityToSupply 
          AND s.QuantityFromSupply <= d.QuantityFromDemand)
 
  UNION ALL
 
  SELECT
    d.DemandID,
    s.SupplyID,
    d.DemandQuantity
      - CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply 
             THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 END
      - CASE WHEN s.QuantityToSupply < d.QuantityToDemand 
             THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity
  FROM #supply AS s 
    INNER JOIN #demand AS d 
      ON (s.QuantityFromSupply < d.QuantityToDemand 
          AND d.QuantityFromDemand < s.QuantityFromSupply);

Como puede ver, está muy cerca de la solución de intersecciones revisada que cubrí.

El plan para la consulta final en la solución de Kamil se muestra en la Figura 8.

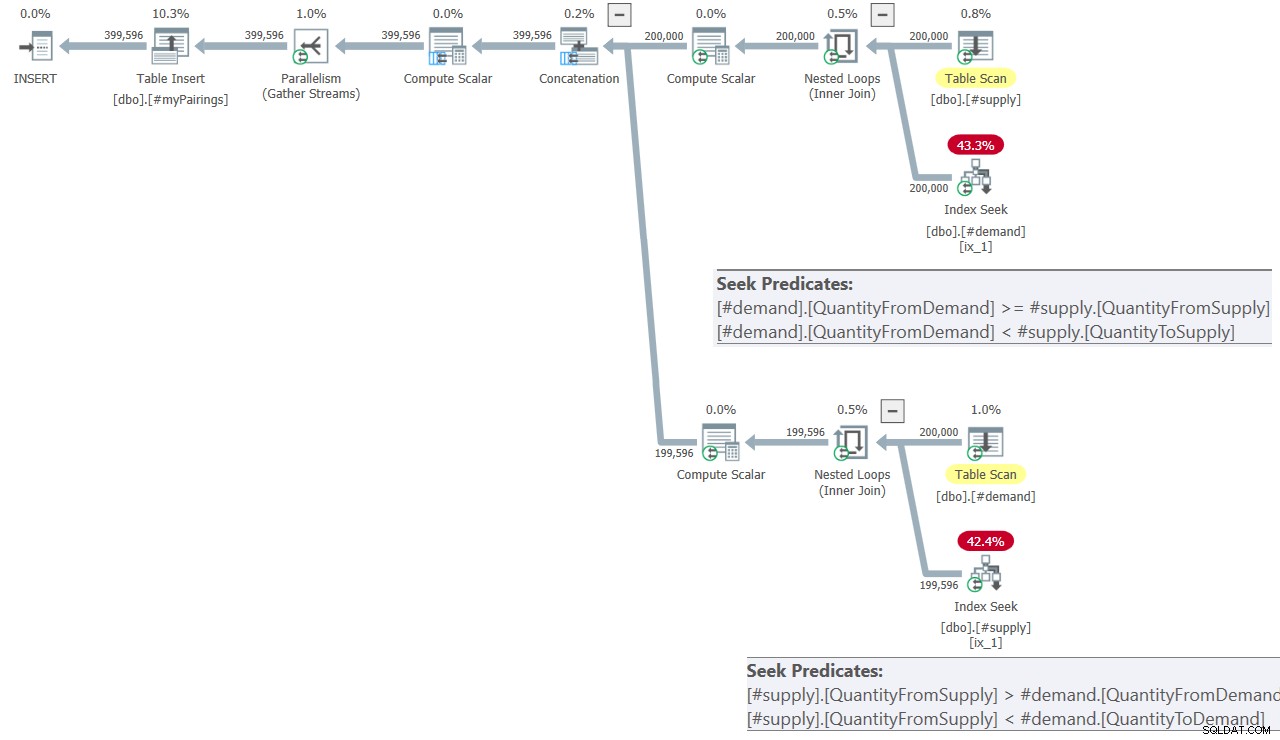
Figura 8:Plan de consulta para la consulta final en la solución de Kamil

El plan se parece bastante al que se muestra anteriormente en la Figura 7.

Prueba de rendimiento

Recuerde que la solución clásica de intersecciones tardó 931 segundos en completarse frente a una entrada con 400 000 filas. ¡Son 15 minutos! Es mucho, mucho peor que la solución del cursor, que tardó unos 12 segundos en completarse con la misma entrada. La Figura 9 tiene los números de rendimiento, incluidas las nuevas soluciones analizadas en este artículo.

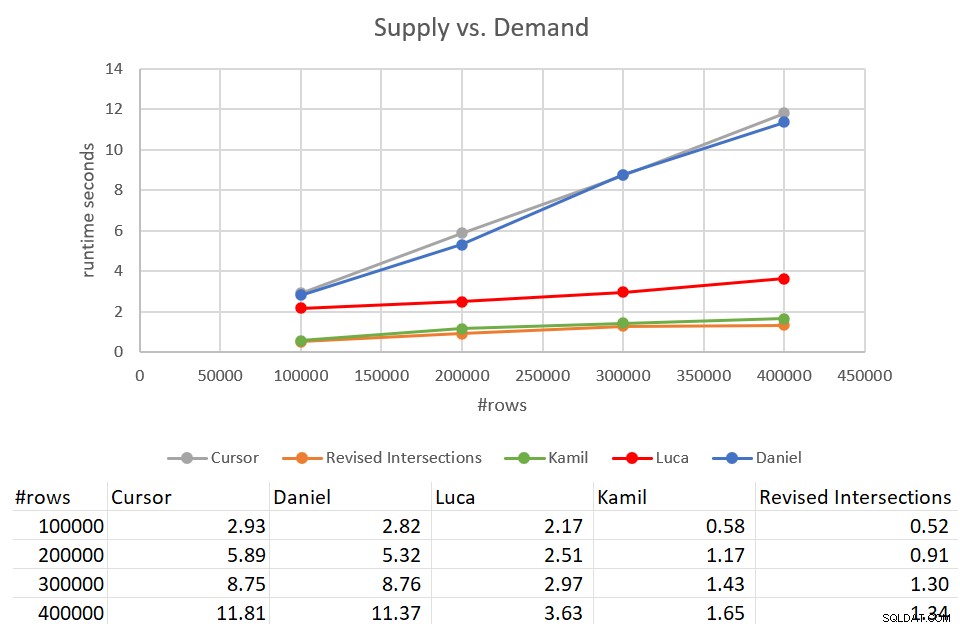
Figura 9:Prueba de rendimiento

Como puede ver, la solución de Kamil y la solución de intersecciones revisada similar tardaron aproximadamente 1,5 segundos en completarse contra la entrada de 400K filas. Esa es una mejora bastante decente en comparación con la solución original basada en cursor. El principal inconveniente de estas soluciones es el costo de E/S. Con una búsqueda por fila, para una entrada de 400 000 filas, estas soluciones realizan un exceso de 1,35 millones de lecturas. Pero también podría considerarse un costo perfectamente aceptable dado el buen tiempo de ejecución y el escalado que obtiene.

¿Qué sigue?

Nuestro primer intento de resolver el desafío de hacer coincidir la oferta con la demanda se basó en la prueba clásica de intersección de intervalos y obtuvo un plan de bajo rendimiento con escala cuadrática. Mucho peor que la solución basada en cursor. Según los conocimientos de Luca, Kamil y Daniel, utilizando una prueba de intersección de intervalo revisada, nuestro segundo intento fue una mejora significativa que utiliza la indexación de manera eficiente y funciona mejor que la solución basada en cursor. Sin embargo, esta solución implica un costo de E/S significativo. El próximo mes continuaré explorando soluciones adicionales.

[ Saltar a:Desafío original | Soluciones:Parte 1 | Parte 2 | Parte 3 ]