Recientemente, mi amigo Erland Sommarskog me presentó un nuevo desafío de islas. Se basa en una pregunta de un foro de base de datos pública. El desafío en sí no es complicado de manejar cuando se utilizan técnicas bien conocidas, que emplean principalmente funciones de ventana. Sin embargo, estas técnicas requieren una clasificación explícita a pesar de la presencia de un índice de apoyo. Esto afecta la escalabilidad y el tiempo de respuesta de las soluciones. Aficionado a los desafíos, me dispuse a encontrar una solución para minimizar la cantidad de operadores Ordenar explícitos en el plan o, mejor aún, eliminar la necesidad de ellos por completo. Y encontré tal solución.
Comenzaré presentando una forma generalizada del desafío. Luego mostraré dos soluciones basadas en técnicas conocidas, seguidas de la nueva solución. Finalmente, compararé el rendimiento de las diferentes soluciones.
Te recomiendo que intentes encontrar una solución antes de implementar la mía.
El desafío
Presentaré una forma generalizada del desafío de las islas originales de Erland.
Use el siguiente código para crear una tabla llamada T1 y complétela con un pequeño conjunto de datos de muestra:
SET NOCOUNT ON;
USE tempdb;
DROP TABLE IF EXISTS dbo.T1
CREATE TABLE dbo.T1
(
grp VARCHAR(10) NOT NULL,
ord INT NOT NULL,
val VARCHAR(10) NOT NULL,
CONSTRAINT PK_T1 PRIMARY KEY(grp, ord)
);
GO
INSERT INTO dbo.T1(grp, ord, val) VALUES
('Group A', 1002, 'Y'),
('Group A', 1003, 'Y'),
('Group A', 1005, 'Y'),
('Group A', 1007, 'N'),
('Group A', 1011, 'N'),
('Group A', 1013, 'N'),
('Group A', 1017, 'Y'),
('Group A', 1019, 'Y'),
('Group A', 1023, 'N'),
('Group A', 1029, 'N'),
('Group B', 1001, 'X'),
('Group B', 1002, 'X'),
('Group B', 1003, 'Z'),
('Group B', 1005, 'Z'),
('Group B', 1008, 'Z'),
('Group B', 1013, 'Z'),
('Group B', 1021, 'Y'),
('Group B', 1034, 'Y'); El reto es el siguiente:
Suponiendo una partición basada en la columna grp y un orden basado en la columna ord, calcule los números de fila secuenciales comenzando con 1 dentro de cada grupo consecutivo de filas con el mismo valor en la columna val. El siguiente es el resultado deseado para el pequeño conjunto dado de datos de muestra:
grp ord val seqno -------- ----- ---- ------ Group A 1002 Y 1 Group A 1003 Y 2 Group A 1005 Y 3 Group A 1007 N 1 Group A 1011 N 2 Group A 1013 N 3 Group A 1017 Y 1 Group A 1019 Y 2 Group A 1023 N 1 Group A 1029 N 2 Group B 1001 X 1 Group B 1002 X 2 Group B 1003 Z 1 Group B 1005 Z 2 Group B 1008 Z 3 Group B 1013 Z 4 Group B 1021 Y 1 Group B 1034 Y 2
Tenga en cuenta la definición de la restricción de clave principal basada en la clave compuesta (grp, ord), que da como resultado un índice agrupado basado en la misma clave. Este índice puede admitir potencialmente funciones de ventana particionadas por grp y ordenadas por ord.
Para probar el rendimiento de su solución, deberá completar la tabla con volúmenes más grandes de datos de muestra. Use el siguiente código para crear la función auxiliar GetNums:
CREATE FUNCTION dbo.GetNums(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1)
rownum AS rn,
@high + 1 - rownum AS op,
@low - 1 + rownum AS n
FROM Nums
ORDER BY rownum;
GO Utilice el siguiente código para completar T1, después de cambiar los parámetros que representan la cantidad de grupos, la cantidad de filas por grupo y la cantidad de valores distintos que desee:
DECLARE
@numgroups AS INT = 1000,
@rowspergroup AS INT = 10000, -- test with 1000 to 10000 here
@uniquevalues AS INT = 5;
ALTER TABLE dbo.T1 DROP CONSTRAINT PK_T1;
TRUNCATE TABLE dbo.T1;
INSERT INTO dbo.T1 WITH(TABLOCK) (grp, ord, val)
SELECT
CAST(G.n AS VARCHAR(10)) AS grp,
CAST(R.n AS INT) AS ord,
CAST(ABS(CHECKSUM(NEWID())) % @uniquevalues + 1 AS VARCHAR(10)) AS val
FROM dbo.GetNums(1, @numgroups) AS G
CROSS JOIN dbo.GetNums(1, @rowspergroup) AS R;
ALTER TABLE dbo.T1 ADD CONSTRAINT PK_T1 PRIMARY KEY CLUSTERED(grp, ord);
En mis pruebas de rendimiento, llené la tabla con 1000 grupos, entre 1000 y 10 000 filas por grupo (de 1 a 10 millones de filas) y 5 valores distintos. Usé un SELECT INTO instrucción para escribir el resultado en una tabla temporal.
Mi máquina de prueba tiene cuatro CPU lógicas que ejecutan SQL Server 2019 Enterprise.
Asumiré que está utilizando un entorno diseñado para admitir el modo por lotes en el almacenamiento de filas, ya sea directamente, por ejemplo, utilizando la edición Enterprise de SQL Server 2019 como la mía, o indirectamente, mediante la creación de un índice de almacén de columnas ficticio en la tabla.
Recuerde, puntos extra si logra encontrar una solución eficiente sin una clasificación explícita en el plan. ¡Buena suerte!
¿Se necesita un operador Ordenar en la optimización de las funciones de ventana?
Antes de cubrir las soluciones, un poco de información sobre optimización para que lo que verá en los planes de consulta más adelante tenga más sentido.
Las técnicas más comunes para resolver tareas de islas como la nuestra involucran el uso de alguna combinación de funciones de ventana de agregación y/o clasificación. SQL Server puede procesar tales funciones de ventana utilizando una serie de operadores de modo de fila más antiguos (Segmento, Proyecto de secuencia, Segmento, Spool de ventana, Agregado de flujo) o el operador Agregado de ventana de modo por lotes más nuevo y generalmente más eficiente.
En ambos casos, los operadores que manejan el cálculo de la función de la ventana necesitan ingerir los datos ordenados por los elementos de partición y ordenación de la ventana. Si no tiene un índice de soporte, naturalmente, SQL Server deberá introducir un operador Ordenar en el plan. Por ejemplo, si tiene múltiples funciones de ventana en su solución con más de una combinación única de partición y ordenación, seguramente tendrá una ordenación explícita en el plan. Pero, ¿qué sucede si solo tiene una combinación única de partición y ordenación y un índice de soporte?
El método de modo de fila más antiguo puede basarse en datos preordenados ingeridos de un índice sin la necesidad de un operador Ordenar explícito en los modos en serie y en paralelo. El operador de modo por lotes más nuevo elimina gran parte de las ineficiencias de la optimización del modo de fila anterior y tiene los beneficios inherentes del procesamiento en modo por lotes. Sin embargo, su implementación paralela actual requiere un operador de clasificación paralelo de modo por lotes intermediario, incluso cuando está presente un índice de soporte. Solo su implementación en serie puede basarse en el orden del índice sin un operador Sort. Todo esto es para decir que cuando el optimizador necesita elegir una estrategia para manejar su función de ventana, suponiendo que tenga un índice de soporte, generalmente será una de las siguientes cuatro opciones:
- Modo fila, serie, sin clasificación
- Modo fila, paralelo, sin clasificación
- Modo por lotes, serie, sin clasificación
- Modo por lotes, paralelo, clasificación
Se elegirá cualquiera que resulte en el costo del plan más bajo, suponiendo, por supuesto, que se cumplan los requisitos previos para el paralelismo y el modo por lotes al considerarlos. Normalmente, para que el optimizador justifique un plan paralelo, los beneficios del paralelismo deben superar el trabajo adicional como la sincronización de subprocesos. Con la opción 4 anterior, los beneficios del paralelismo deben superar el trabajo adicional habitual relacionado con el paralelismo, además de la clasificación adicional.
Mientras experimentaba con diferentes soluciones para nuestro desafío, tuve casos en los que el optimizador eligió la opción 2 anterior. Lo eligió a pesar de que el método de modo fila implica algunas ineficiencias porque los beneficios del paralelismo y la ausencia de clasificación resultaron en un plan con un costo menor que las alternativas. En algunos de esos casos, forzar un plan en serie con una sugerencia resultó en la opción 3 anterior y en un mejor rendimiento.
Con estos antecedentes en mente, veamos soluciones. Comenzaré con dos soluciones que se basan en técnicas conocidas para tareas de islas que no pueden escapar de la clasificación explícita en el plan.
Solución basada en técnica conocida 1
La siguiente es la primera solución a nuestro desafío, que se basa en una técnica que se conoce desde hace tiempo:
WITH C AS
(
SELECT *,
ROW_NUMBER() OVER(PARTITION BY grp ORDER BY ord) -
ROW_NUMBER() OVER(PARTITION BY grp, val ORDER BY ord) AS island
FROM dbo.T1
)
SELECT grp, ord, val,
ROW_NUMBER() OVER(PARTITION BY grp, val, island ORDER BY ord) AS seqno
FROM C; Me referiré a ella como Solución Conocida 1.
El CTE denominado C se basa en una consulta que calcula dos números de fila. El primero (me referiré a él como rn1) está dividido por grp y ordenado por ord. El segundo (me referiré a él como rn2) está dividido por grp y val y ordenado por ord. Dado que rn1 tiene espacios entre diferentes grupos del mismo valor y rn2 no, la diferencia entre rn1 y rn2 (columna llamada isla) es un valor constante único para todas las filas con los mismos valores de grp y valor. El siguiente es el resultado de la consulta interna, incluidos los resultados de los cálculos numéricos de dos filas, que no se devuelven como columnas separadas:
grp ord val rn1 rn2 island -------- ----- ---- ---- ---- ------- Group A 1002 Y 1 1 0 Group A 1003 Y 2 2 0 Group A 1005 Y 3 3 0 Group A 1007 N 4 1 3 Group A 1011 N 5 2 3 Group A 1013 N 6 3 3 Group A 1017 Y 7 4 3 Group A 1019 Y 8 5 3 Group A 1023 N 9 4 5 Group A 1029 N 10 5 5 Group B 1001 X 1 1 0 Group B 1002 X 2 2 0 Group B 1003 Z 3 1 2 Group B 1005 Z 4 2 2 Group B 1008 Z 5 3 2 Group B 1013 Z 6 4 2 Group B 1021 Y 7 1 6 Group B 1034 Y 8 2 6
Lo que le queda por hacer a la consulta externa es calcular la columna de resultados seqno usando la función ROW_NUMBER, dividida por grp, val e island, y ordenada por ord, generando el resultado deseado.
Tenga en cuenta que puede obtener el mismo valor de isla para diferentes valores de val dentro de la misma partición, como en el resultado anterior. Esta es la razón por la que es importante usar grp, val e island como elementos de partición de ventana y no grp e island solos.
De manera similar, si se trata de una tarea de islas que requiere que agrupe los datos por isla y calcule los agregados del grupo, agruparía las filas por grp, val e island. Pero este no es el caso de nuestro desafío. Aquí se le asignó la tarea de calcular los números de fila de forma independiente para cada isla.
La figura 1 tiene el plan predeterminado que obtuve para esta solución en mi máquina después de completar la tabla con 10 millones de filas.
Figura 1:Plan paralelo para la Solución conocida 1
El cálculo de rn1 puede basarse en el orden del índice. Por lo tanto, el optimizador eligió la estrategia sin clasificación + modo de filas paralelas para este (primer segmento y operadores de proyecto de secuencia en el plan). Dado que los cálculos de rn2 y seqno utilizan sus propias combinaciones únicas de elementos de partición y ordenación, la clasificación explícita es inevitable para aquellos, independientemente de la estrategia utilizada. Por lo tanto, el optimizador eligió la estrategia de ordenación + modo por lotes en paralelo para ambos. Este plan implica dos operadores de clasificación explícitos.
En mi prueba de rendimiento, esta solución tardó 3,68 segundos en completarse frente a 1 millón de filas y 43,1 segundos frente a 10 millones de filas.
Como se mencionó, probé todas las soluciones también forzando un plan en serie (con una sugerencia de MAXDOP 1). El plan de serie para esta solución se muestra en la Figura 1.
Figura 2:Plan en serie para la solución conocida 1
Como era de esperar, esta vez también el cálculo de rn1 usa la estrategia de modo por lotes sin un operador de clasificación anterior, pero el plan todavía tiene dos operadores de clasificación para los cálculos de número de fila subsiguientes. El plan en serie funcionó peor que el paralelo en mi máquina con todos los tamaños de entrada que probé, tardando 4,54 segundos en completarse con 1 millón de filas y 61,5 segundos con 10 millones de filas.
Solución basada en técnica conocida 2
La segunda solución que presentaré se basa en una técnica brillante para la detección de islas que aprendí de Paul White hace unos años. A continuación se muestra el código de solución completo basado en esta técnica:
WITH C1 AS
(
SELECT *,
CASE
WHEN val = LAG(val) OVER(PARTITION BY grp ORDER BY ord) THEN 0
ELSE 1
END AS isstart
FROM dbo.T1
),
C2 AS
(
SELECT *,
SUM(isstart) OVER(PARTITION BY grp ORDER BY ord ROWS UNBOUNDED PRECEDING) AS island
FROM C1
)
SELECT grp, ord, val,
ROW_NUMBER() OVER(PARTITION BY grp, island ORDER BY ord) AS seqno
FROM C2; Me referiré a esta solución como Solución Conocida 2.
La consulta que define los cálculos de CTE C1 utiliza una expresión CASE y la función de ventana LAG (particionada por grp y ordenada por ord) para calcular una columna de resultados llamada isstart. Esta columna tiene el valor 0 cuando el valor del valor actual es el mismo que el anterior y 1 en caso contrario. En otras palabras, es 1 cuando la fila es la primera de una isla y 0 en caso contrario.
El siguiente es el resultado de la consulta que define C1:
grp ord val isstart -------- ----- ---- -------- Group A 1002 Y 1 Group A 1003 Y 0 Group A 1005 Y 0 Group A 1007 N 1 Group A 1011 N 0 Group A 1013 N 0 Group A 1017 Y 1 Group A 1019 Y 0 Group A 1023 N 1 Group A 1029 N 0 Group B 1001 X 1 Group B 1002 X 0 Group B 1003 Z 1 Group B 1005 Z 0 Group B 1008 Z 0 Group B 1013 Z 0 Group B 1021 Y 1 Group B 1034 Y 0
La magia en lo que a detección de islas se refiere ocurre en el CTE C2. La consulta que lo define calcula un identificador de isla utilizando la función de ventana SUM (también particionada por grp y ordenada por ord) aplicada a la columna isstart. La columna de resultado con el identificador de isla se llama isla. Dentro de cada partición, obtiene 1 para la primera isla, 2 para la segunda isla y así sucesivamente. Entonces, la combinación de columnas grp e isla es un identificador de isla, que puede usar en tareas de islas que implican agrupar por isla cuando sea relevante.
El siguiente es el resultado de la consulta que define C2:
grp ord val isstart island -------- ----- ---- -------- ------- Group A 1002 Y 1 1 Group A 1003 Y 0 1 Group A 1005 Y 0 1 Group A 1007 N 1 2 Group A 1011 N 0 2 Group A 1013 N 0 2 Group A 1017 Y 1 3 Group A 1019 Y 0 3 Group A 1023 N 1 4 Group A 1029 N 0 4 Group B 1001 X 1 1 Group B 1002 X 0 1 Group B 1003 Z 1 2 Group B 1005 Z 0 2 Group B 1008 Z 0 2 Group B 1013 Z 0 2 Group B 1021 Y 1 3 Group B 1034 Y 0 3
Por último, la consulta externa calcula la columna de resultados deseada seqno con una función ROW_NUMBER, dividida por grp e island, y ordenada por ord. Observe que esta combinación de elementos de partición y ordenación es diferente de la utilizada por las funciones de ventana anteriores. Mientras que el cálculo de las dos primeras funciones de ventana puede basarse potencialmente en el orden del índice, la última no.
La Figura 3 tiene el plan predeterminado que obtuve para esta solución.
Figura 3:Plan paralelo para la solución conocida 2
Como puede ver en el plan, el cálculo de las dos primeras funciones de ventana utiliza la estrategia de modo sin ordenación + filas paralelas, y el cálculo de la última utiliza la estrategia de modo ordenación + lotes paralelos.
Los tiempos de ejecución que obtuve para esta solución oscilaron entre 2,57 segundos frente a 1 millón de filas y 46,2 segundos frente a 10 millones de filas.
Al forzar el procesamiento en serie, obtuve el plan que se muestra en la Figura 4.
Figura 4:Plan serial para la Solución conocida 2
Como era de esperar, esta vez todos los cálculos de funciones de ventana se basan en la estrategia del modo por lotes. Los dos primeros sin clasificación previa, y el último con. Tanto el plan paralelo como el serial involucraban un operador Ordenar explícito. El plan en serie funcionó mejor que el plan en paralelo en mi máquina con los tamaños de entrada que probé. Los tiempos de ejecución que obtuve para el plan en serie forzado variaron de 1,75 segundos contra 1 millón de filas a 21,7 segundos contra 10 millones de filas.
Solución basada en nueva técnica
Cuando Erland presentó este desafío en un foro privado, la gente se mostró escéptica sobre la posibilidad de resolverlo con una consulta que había sido optimizada con un plan sin clasificación explícita. Eso es todo lo que necesitaba escuchar para motivarme. Entonces, esto es lo que se me ocurrió:
WITH C1 AS
(
SELECT *,
ROW_NUMBER() OVER(PARTITION BY grp ORDER BY ord) AS rn,
LAG(val) OVER(PARTITION BY grp ORDER BY ord) AS prev
FROM dbo.T1
),
C2 AS
(
SELECT *,
MAX(CASE WHEN val = prev THEN NULL ELSE rn END)
OVER(PARTITION BY grp ORDER BY ord ROWS UNBOUNDED PRECEDING) AS firstrn
FROM C1
)
SELECT grp, ord, val, rn - firstrn + 1 AS seqno
FROM C2; La solución utiliza tres funciones de ventana:LAG, ROW_NUMBER y MAX. Lo importante aquí es que los tres se basan en la partición grp y el orden de pedido, que está alineado con el orden de clave de índice de soporte.
La consulta que define el CTE C1 utiliza la función ROW_NUMBER para calcular los números de fila (columna rn) y la función LAG para devolver el valor de valor anterior (columna anterior).
Aquí está el resultado de la consulta que define C1:
grp ord val rn prev -------- ----- ---- --- ----- Group A 1002 Y 1 NULL Group A 1003 Y 2 Y Group A 1005 Y 3 Y Group A 1007 N 4 Y Group A 1011 N 5 N Group A 1013 N 6 N Group A 1017 Y 7 N Group A 1019 Y 8 Y Group A 1023 N 9 Y Group A 1029 N 10 N Group B 1001 X 1 NULL Group B 1002 X 2 X Group B 1003 Z 3 X Group B 1005 Z 4 Z Group B 1008 Z 5 Z Group B 1013 Z 6 Z Group B 1021 Y 7 Z Group B 1034 Y 8 Y
Observe cuando val y prev son iguales, no es la primera fila de la isla, de lo contrario lo es.
Según esta lógica, la consulta que define el CTE C2 utiliza una expresión CASE que devuelve rn cuando la fila es la primera de una isla y NULL en caso contrario. Luego, el código aplica la función de ventana MAX al resultado de la expresión CASE, devolviendo el primer rn de la isla (primera columna rn).
Este es el resultado de la consulta que define C2, incluido el resultado de la expresión CASE:
grp ord val rn prev CASE firstrn -------- ----- ---- --- ----- ----- -------- Group A 1002 Y 1 NULL 1 1 Group A 1003 Y 2 Y NULL 1 Group A 1005 Y 3 Y NULL 1 Group A 1007 N 4 Y 4 4 Group A 1011 N 5 N NULL 4 Group A 1013 N 6 N NULL 4 Group A 1017 Y 7 N 7 7 Group A 1019 Y 8 Y NULL 7 Group A 1023 N 9 Y 9 9 Group A 1029 N 10 N NULL 9 Group B 1001 X 1 NULL 1 1 Group B 1002 X 2 X NULL 1 Group B 1003 Z 3 X 3 3 Group B 1005 Z 4 Z NULL 3 Group B 1008 Z 5 Z NULL 3 Group B 1013 Z 6 Z NULL 3 Group B 1021 Y 7 Z 7 7 Group B 1034 Y 8 Y NULL 7
Lo que queda para la consulta externa es calcular la columna de resultado deseada seqno como rn menos firstrn plus 1.
La Figura 5 tiene el plan paralelo predeterminado que obtuve para esta solución cuando la probé usando una declaración SELECT INTO, escribiendo el resultado en una tabla temporal.
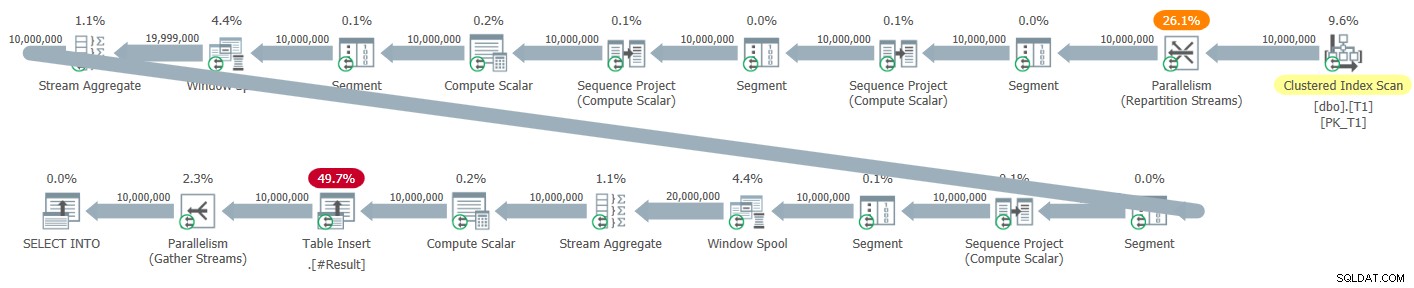Figura 5:Plan paralelo para una nueva solución
No hay operadores de clasificación explícitos en este plan. Sin embargo, las tres funciones de ventana se calculan utilizando la estrategia de modo de filas paralelas + sin clasificación, por lo que nos estamos perdiendo los beneficios del procesamiento por lotes. Los tiempos de ejecución que obtuve para esta solución con el plan paralelo oscilaron entre 2,47 segundos contra 1 millón de filas y 41,4 contra 10 millones de filas.
Aquí, existe una gran probabilidad de que un plan en serie con procesamiento por lotes funcione significativamente mejor, especialmente cuando la máquina no tiene muchas CPU. Recuerde que estoy probando mis soluciones en una máquina con 4 CPU lógicas. La figura 6 tiene el plan que obtuve para esta solución al forzar el procesamiento en serie.
Figura 6:Plan serial para una nueva solución
Las tres funciones de ventana utilizan la estrategia de modo de lotes en serie + sin clasificación. Y los resultados son bastante impresionantes. Los tiempos de ejecución de esta solución oscilaron entre 0,5 segundos frente a 1 millón de filas y 5,49 segundos frente a 10 millones de filas. Lo que también es curioso acerca de esta solución es que al probarla como una declaración SELECT normal (con resultados descartados) en lugar de una declaración SELECT INTO, SQL Server eligió el plan en serie de forma predeterminada. Con las otras dos soluciones, obtuve un plan paralelo por defecto tanto con SELECT como con SELECT INTO.
Consulte la siguiente sección para obtener los resultados completos de la prueba de rendimiento.
Comparación de rendimiento
Aquí está el código que usé para probar las tres soluciones, por supuesto, sin comentar la sugerencia de MAXDOP 1 para probar los planes en serie:
-- Test Known Solution 1
DROP TABLE IF EXISTS #Result;
WITH C AS
(
SELECT *,
ROW_NUMBER() OVER(PARTITION BY grp ORDER BY ord) -
ROW_NUMBER() OVER(PARTITION BY grp, val ORDER BY ord) AS island
FROM dbo.T1
)
SELECT grp, ord, val,
ROW_NUMBER() OVER(PARTITION BY grp, val, island ORDER BY ord) AS seqno
INTO #Result
FROM C
/* OPTION(MAXDOP 1) */; -- uncomment for serial test
GO
-- Test Known Solution 2
DROP TABLE IF EXISTS #Result;
WITH C1 AS
(
SELECT *,
CASE
WHEN val = LAG(val) OVER(PARTITION BY grp ORDER BY ord) THEN 0
ELSE 1
END AS isstart
FROM dbo.T1
),
C2 AS
(
SELECT *,
SUM(isstart) OVER(PARTITION BY grp ORDER BY ord ROWS UNBOUNDED PRECEDING) AS island
FROM C1
)
SELECT grp, ord, val,
ROW_NUMBER() OVER(PARTITION BY grp, island ORDER BY ord) AS seqno
INTO #Result
FROM C2
/* OPTION(MAXDOP 1) */;
GO
-- Test New Solution
DROP TABLE IF EXISTS #Result;
WITH C1 AS
(
SELECT *,
ROW_NUMBER() OVER(PARTITION BY grp ORDER BY ord) AS rn,
LAG(val) OVER(PARTITION BY grp ORDER BY ord) AS prev
FROM dbo.T1
),
C2 AS
(
SELECT *,
MAX(CASE WHEN val = prev THEN NULL ELSE rn END)
OVER(PARTITION BY grp ORDER BY ord ROWS UNBOUNDED PRECEDING) AS firstrn
FROM C1
)
SELECT grp, ord, val, rn - firstrn + 1 AS seqno
INTO #Result
FROM C2
/* OPTION(MAXDOP 1) */; La Figura 7 tiene los tiempos de ejecución de los planes en serie y en paralelo para todas las soluciones frente a diferentes tamaños de entrada.
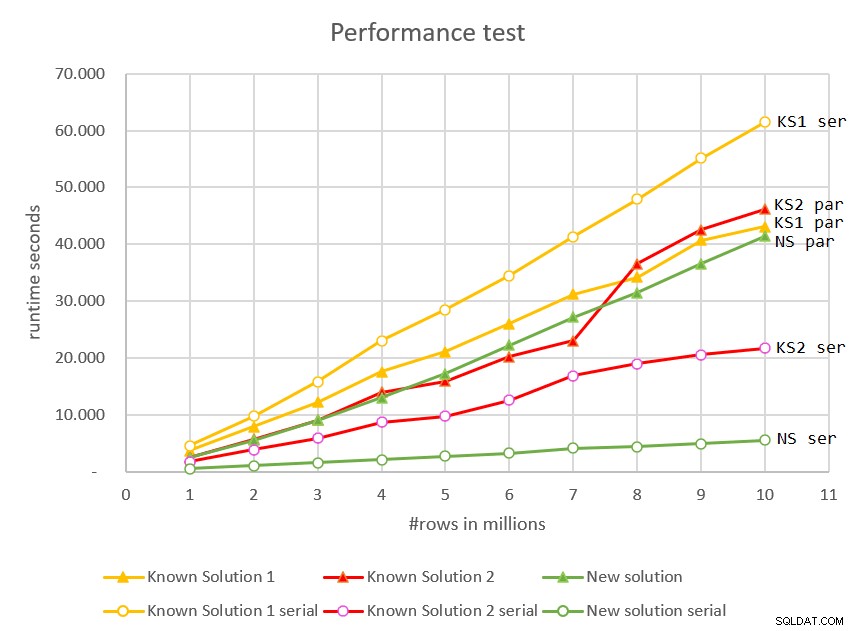Figura 7:Comparación de rendimiento
La nueva solución, que utiliza el modo serie, es la clara ganadora. Tiene un gran rendimiento, escalado lineal y tiempo de respuesta inmediato.
Conclusión
Las tareas de islas son bastante comunes en la vida real. Muchos de ellos implican tanto la identificación de islas como la agrupación de datos por isla. El desafío de las islas de Erland, en el que se centró este artículo, es un poco más exclusivo porque no implica agrupar, sino secuenciar las filas de cada isla con números de fila.
Presenté dos soluciones basadas en técnicas conocidas para identificar islas. El problema con ambos es que dan como resultado planes que implican una clasificación explícita, lo que afecta negativamente el rendimiento, la escalabilidad y el tiempo de respuesta de las soluciones. También presenté una nueva técnica que resultó en un plan sin ningún tipo de clasificación. El plan en serie para esta solución, que utiliza una estrategia sin ordenación + modo por lotes en serie, tiene un excelente rendimiento, escala lineal y tiempo de respuesta inmediato. Es desafortunado, al menos por ahora, no podemos tener una estrategia de modo por lotes paralelo + sin clasificación para manejar funciones de ventana.
